filmov
tv
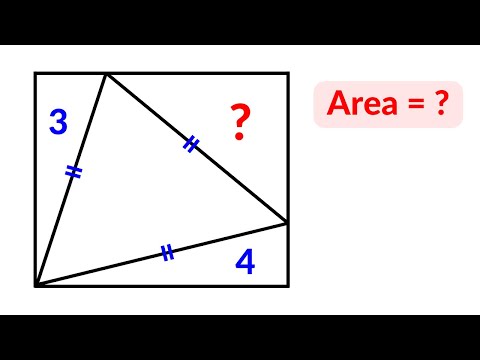
Russian Math Olympiad | A Very Nice Geometry Problem | Find the area of the square

Показать описание
GET MY EBOOKS
•••••••••••••••••••••••
OTHER CHAPTERS : COMING SOON.....
--------------------------------------------------------------------------------
Join the channel to become a member
•••••••••••••••••••••••
OTHER CHAPTERS : COMING SOON.....
--------------------------------------------------------------------------------
Join the channel to become a member
Russian Math Olympiad | A Very Nice Geometry Problem | Find the area of the square
Russia | Math Olympiad Question | You should know this trick!!
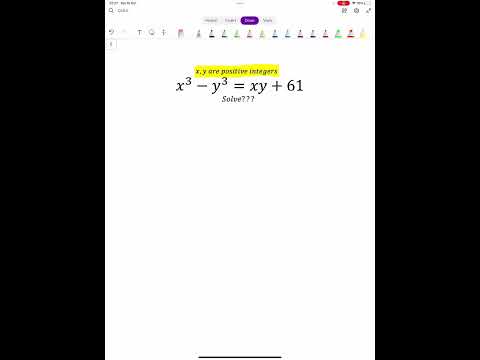
Find all integer solutions (Russian Math Olympiad)
Russian Math Olympiad | A Very Nice Geometry Problem
Russian Math Olympiad Question
Russian Math Olympiad - Math Contest
Russian Math Olympiad | A Very Nice Geometry Problem
Russian Math Olympiad | A Very Nice Geometry Problem
Germany | Can you solve this? A Nice Maths Olympiad Algebra problem #maths #algebra
Day 2 All-Russian Math Olympiad 2013 | Discrete Mathematics | Math Olympiad Training
Russian Olympiad Mathematics | Exponential equation.
Russian Math Olympiad | A Very Nice Geometry Problem | 2 Different Methods
Math Olympiad Challenge | Russian Math Olympiad...
Russian Math Olympiad Geometry Problem | Best Math Olympiad Problems | 2 Different Methods To Solve
Russian Math Olympiad Problem | A Very Nice Geometry Challenge | 2 Different Methods
This Russian Math Olympiad Problem Will Blow Your Mind
Russian Maths Olympiads
Russian Math Olympiad | Best Geometry Problems
Russian 🇷🇺 Maths Olympiad Question | #shorts #maths #mathstricks #exponents #olympiad #yt #russia...
Russian Math Olympiad | A Very Nice Geometry Problem | 2 Different Methods
Russian | You should know this | Math Olympiad Trick
26th RUSSIAN MATH OLYMPIAD PROBLEM WHAT IS a+b+c 01E
The Russian | Diophantine Equation | Russian Math Olympiad
Russian Maths Olympiad 1996 Q4 | Math Olympiad Training
Комментарии
 0:13:23
0:13:23
 0:08:01
0:08:01
 0:20:56
0:20:56
 0:14:39
0:14:39
 0:03:42
0:03:42
 0:03:57
0:03:57
 0:14:34
0:14:34
 0:11:29
0:11:29
 0:04:31
0:04:31
 0:01:11
0:01:11
 0:07:21
0:07:21
 0:19:49
0:19:49
 0:03:06
0:03:06
 0:24:49
0:24:49
 0:27:41
0:27:41
 0:09:19
0:09:19
 0:00:12
0:00:12
 0:09:58
0:09:58
 0:00:57
0:00:57
 0:19:04
0:19:04
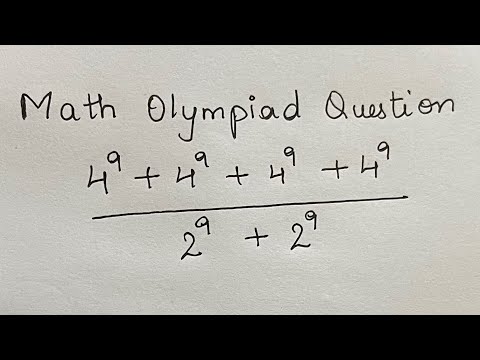 0:01:26
0:01:26
 0:08:03
0:08:03
 0:05:33
0:05:33
 0:06:41
0:06:41