filmov
tv
Square Root of 2 is Irrational
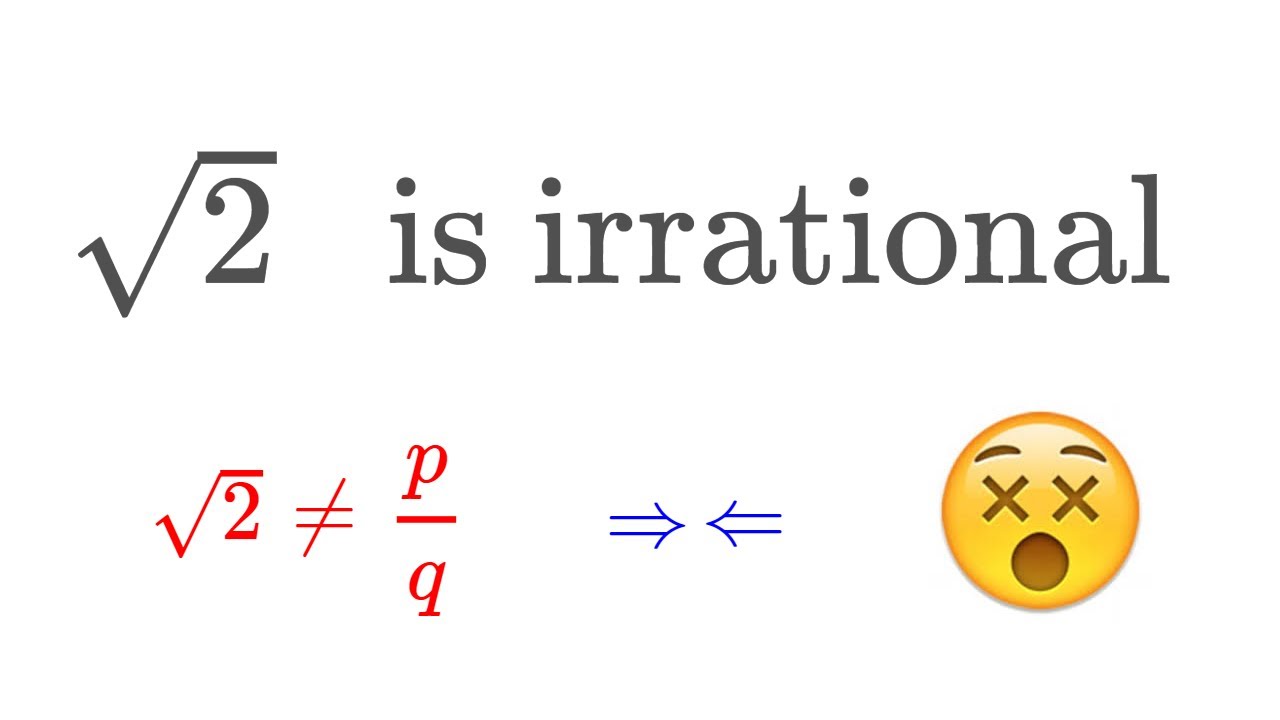
Показать описание
Square root of 2 is irrational
In this video, I present the classic proof that square root of 2 is irrational, by using a proof of contradiction. Featured is also a special fluffy guest :)
In this video, I present the classic proof that square root of 2 is irrational, by using a proof of contradiction. Featured is also a special fluffy guest :)
A Proof That The Square Root of Two Is Irrational
Root 2 - Numberphile
Square Root of 2
Proof: Square Root of 2 is Irrational
Proof that square root of 2 is irrational | Algebra I | Khan Academy
The Square Root of Two: Why it Matters
Proof that Square Root 2 is Irrational
Square Root of 2 is Irrational
How to simplify square root
The Square Root of Two
my favorite way of proving that the square root of 2 is irrational!
How to find square root of 2
Is square root of 2 equal to 2? (Spoiler : no)
Represent root 2 on number line | Root 2 on number line | Locate root 2 on number line
How to Find the Square Root of 2 by Long Division / Square root of 2 / Long Division Method
What is the square root of two? | The Fundamental Theorem of Galois Theory
How to Find Value of Irrational Numbers correct to three decimal places Square root 2 without calcul
The 5 Best Proofs that the Square Root of 2 is Irrational
🔶02 - Show that Square Root of 2 is irrational
This Will Be Your Favorite Simple Problem
Square Root Math Hack
The square root of a square
How To Approximate The Value Of The Square Root Of 2
What are Square Roots? | Math with Mr. J
Комментарии
 0:17:22
0:17:22
 0:08:49
0:08:49
 0:01:30
0:01:30
 0:04:02
0:04:02
 0:07:47
0:07:47
 0:04:56
0:04:56
 0:06:56
0:06:56
 0:10:35
0:10:35
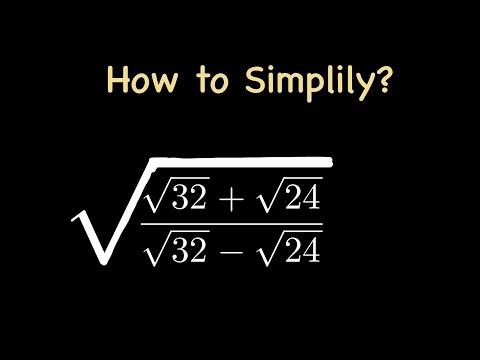 0:05:53
0:05:53
 0:02:40
0:02:40
 0:04:13
0:04:13
 0:03:48
0:03:48
 0:00:59
0:00:59
 0:00:50
0:00:50
 0:06:41
0:06:41
 0:25:10
0:25:10
 0:08:35
0:08:35
 0:04:57
0:04:57
 0:07:49
0:07:49
 0:03:03
0:03:03
 0:00:23
0:00:23
 0:03:43
0:03:43
 0:07:09
0:07:09
 0:04:00
0:04:00