filmov
tv
Fundamental theorem of Algebra - A Simple but Beautiful Geometric proof
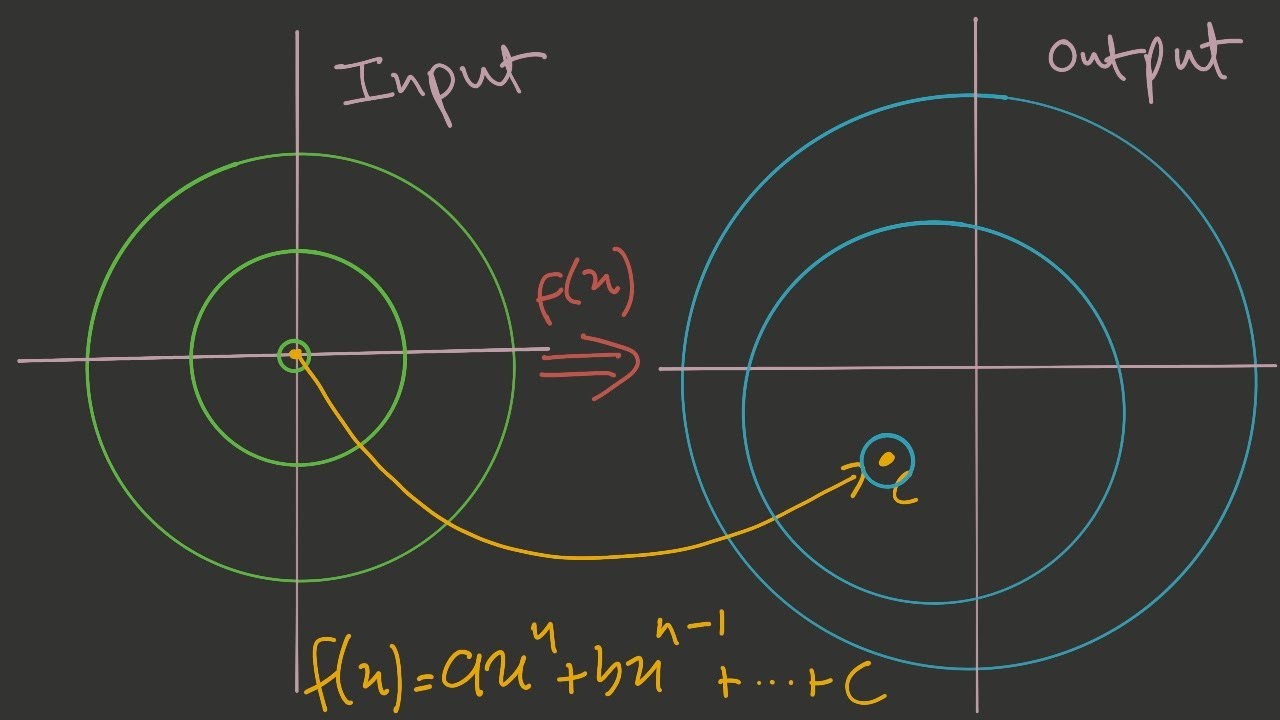
Показать описание
Proof that any polynomial with degree n has exactly n roots.
Time stamps :
0:00 Terms and Definitions
3:25 Complex Number Multiplication
8:34 Proof
Time stamps :
0:00 Terms and Definitions
3:25 Complex Number Multiplication
8:34 Proof
Fundamental Theorem of Algebra
Fundamental Theorem of Algebra - Numberphile
Fundamental theorem of algebra | Polynomial and rational functions | Algebra II | Khan Academy
A Simple and Beautiful proof of The Fundamental Theorem of Algebra
The Fundamental Theorem of Algebra
Fundamental Theorem of Algebra
What does the fundamental theorem of algebra tell us about a polynomial
Fundamental Theorem of Algebra
Fundamental Theorem of Algebra
Intro to COMPLEX NUMBERS // Motivation, Algebraic Definition & Fundamental Theorem of Algebra Ep...
The Fundamental Theorem of Algebra
Fundamental Theorem of Algebra Importance : Math Equations & More
Fundamental theorem of Algebra - A Simple but Beautiful Geometric proof
The Fundamental Theorem of Algebra
Fundamental Theorem of Algebra and Application (example)
Complex Analysis: Fundamental Theorem of Algebra
What is the Fundamental theorem of Algebra, really? | Abstract Algebra Math Foundations 217
Fundamental theorem of algebra for quadratic | Algebra II | Khan Academy
Fundamental Theorem of Algebra
Fundamental Theorem of Algebra Proof | Abstract Algebra |Maths |Mad Teacher
Galois theory: Fundamental theorem of algebra
Using the Fundamental Theorem of Algebra
The fundamental dream of algebra | Abstract Algebra Math Foundations 216 | NJ Wildberger
Rouche's Theorem and the Fundamental Theorem of Algebra
Комментарии
 0:11:07
0:11:07
 0:15:26
0:15:26
 0:05:34
0:05:34
 0:01:28
0:01:28
 0:17:32
0:17:32
 0:04:18
0:04:18
 0:02:34
0:02:34
 0:01:55
0:01:55
 0:21:22
0:21:22
 0:12:00
0:12:00
 0:31:59
0:31:59
 0:01:52
0:01:52
 0:13:22
0:13:22
 0:08:30
0:08:30
 0:05:01
0:05:01
 0:11:37
0:11:37
 0:28:27
0:28:27
 0:06:35
0:06:35
 0:10:42
0:10:42
 0:06:10
0:06:10
 0:12:43
0:12:43
 0:14:28
0:14:28
 0:27:19
0:27:19
 0:11:27
0:11:27