filmov
tv
The Fundamental Theorem of Algebra
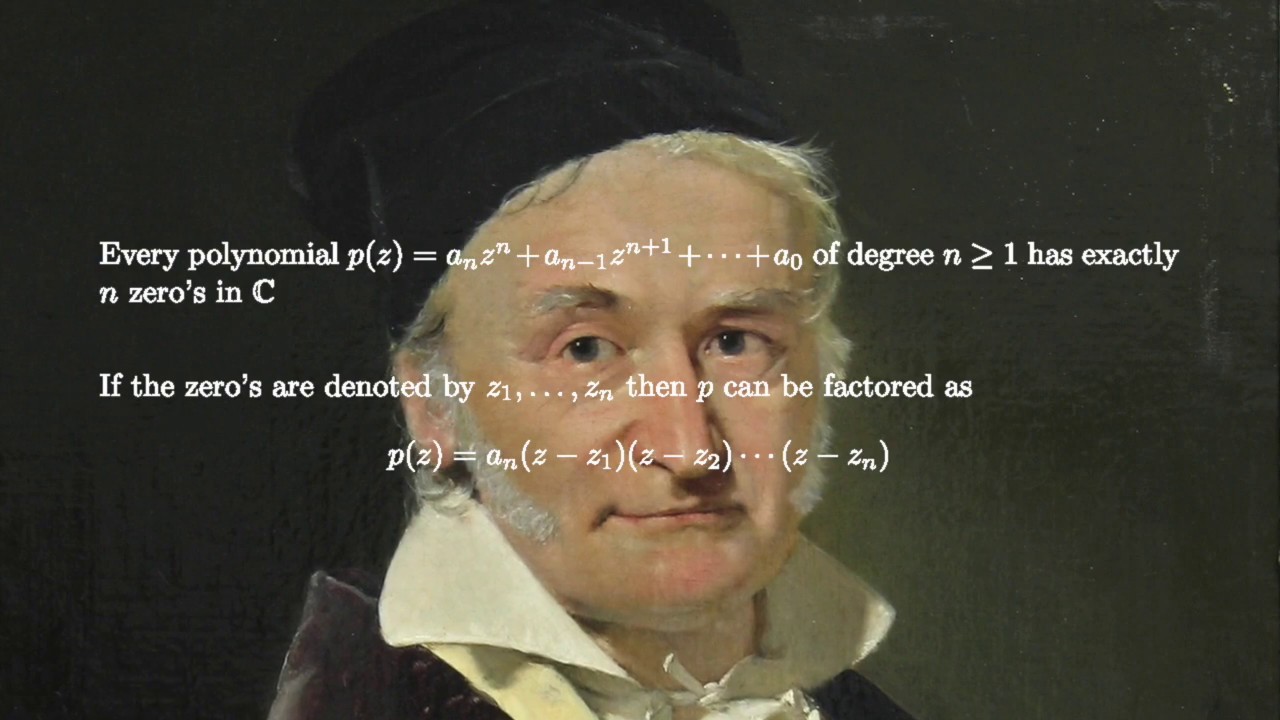
Показать описание
The fact that polynomials are complex analytic in the entire complex plane lies at the heart of a beautiful and simple proof of the fundamental theorem of algebra.
Although it might appear like we are hiding the complexity of the proof by building up so much machinery that it's possible dispose of this mighty theorem in a few lines, in fact it is truly direct. For the most powerful ideas are necessarily the simplest; if they were not simple it would not be possible for them to explain so much.
[1] Complex Analysis, Elias M. Stein, Rami Shakarchi (Chapters 1 & 2)
[2] A Course of Modern Analysis, E. T. Whittaker, G. N. Watson (Chapter 5)
[3] Geometry and the Imagination, David Hilbert, Stephan Cohn-Vossen (Chapter 4, section 38)
Although it might appear like we are hiding the complexity of the proof by building up so much machinery that it's possible dispose of this mighty theorem in a few lines, in fact it is truly direct. For the most powerful ideas are necessarily the simplest; if they were not simple it would not be possible for them to explain so much.
[1] Complex Analysis, Elias M. Stein, Rami Shakarchi (Chapters 1 & 2)
[2] A Course of Modern Analysis, E. T. Whittaker, G. N. Watson (Chapter 5)
[3] Geometry and the Imagination, David Hilbert, Stephan Cohn-Vossen (Chapter 4, section 38)
Fundamental Theorem of Algebra
Fundamental Theorem of Algebra - Numberphile
Fundamental theorem of algebra | Polynomial and rational functions | Algebra II | Khan Academy
The Fundamental Theorem of Algebra
A Simple and Beautiful proof of The Fundamental Theorem of Algebra
What does the fundamental theorem of algebra tell us about a polynomial
Fundamental Theorem of Algebra
Fundamental Theorem of Algebra
The Fundamental Theorem of Algebra
The Fundamental Theorem of Algebra
Fundamental Theorem of Algebra
Fundamental theorem of algebra for quadratic | Algebra II | Khan Academy
Intro to COMPLEX NUMBERS // Motivation, Algebraic Definition & Fundamental Theorem of Algebra Ep...
Fundamental theorem of Algebra - A Simple but Beautiful Geometric proof
Using the Fundamental Theorem of Algebra
Fundamental Theorem of Algebra and Application (example)
Fundamental Theorem of Algebra Importance : Math Equations & More
The Fundamental Theorem of Algebra PT 1
What is the Fundamental theorem of Algebra, really? | Abstract Algebra Math Foundations 217
Fundamental Theorem of Algebra Proof | Abstract Algebra |Maths |Mad Teacher
Fundamental Theorem of Algebra
Complex Analysis: Fundamental Theorem of Algebra
Galois theory: Fundamental theorem of algebra
5-6 The Fundamental Theorem of Algebra
Комментарии
 0:11:07
0:11:07
 0:15:26
0:15:26
 0:05:34
0:05:34
 0:17:32
0:17:32
 0:01:28
0:01:28
 0:02:34
0:02:34
 0:01:55
0:01:55
 0:21:22
0:21:22
 0:08:30
0:08:30
 0:31:59
0:31:59
 0:04:18
0:04:18
 0:06:35
0:06:35
 0:12:00
0:12:00
 0:13:22
0:13:22
 0:14:28
0:14:28
 0:05:01
0:05:01
 0:01:52
0:01:52
 0:11:07
0:11:07
 0:28:27
0:28:27
 0:06:10
0:06:10
 0:10:42
0:10:42
 0:11:37
0:11:37
 0:12:43
0:12:43
 0:33:39
0:33:39