Quantum mechanical simulation of the cyclotron motion of an electron confined under a magnetic field

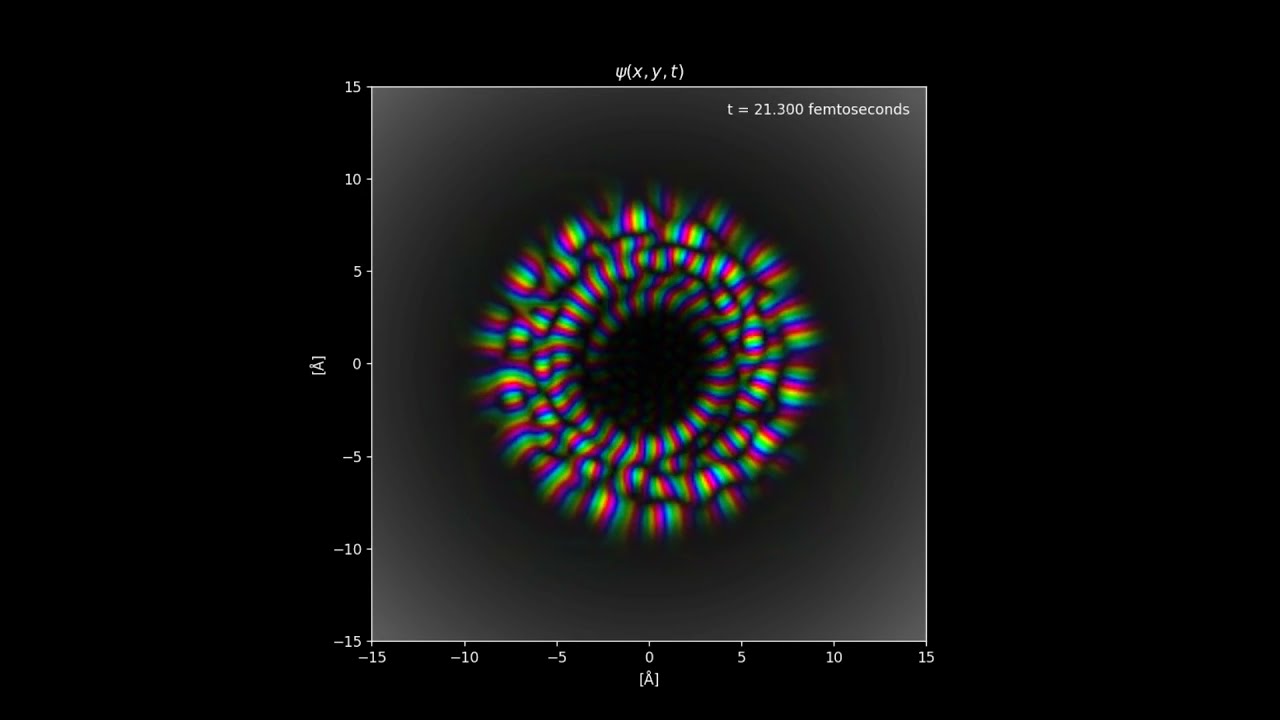
Quantum mechanical simulation of the cyclotron motion of an electron confined under a strong, uniform magnetic field, made by solving the Schrödinger equation. As time passes, the wavepacket spatial distribution disperses until it finally reaches a stationary state with a fixed radial length.

In the visualization, the color hue shows the phase of the wave function of the electron ψ(x,y, t), while the opacity shows the amplitude.

In the example, the magnetic field is uniform over the entire plane and points downwards. If the magnetic field points upwards, the electron would orbit counterclockwise. Notice that we needed a magnetic field of the order of thousands of Teslas to confine the electron in such a small orbit (of the order of Angstroms), but a similar result can be obtained with a weaker magnetic field and therefore larger cyclotron radius.

The resulting wavefunction is just a superposition of these eigenstates. Because the eigenstates decay in the center, the time-dependent version would also. It's also interesting to notice that the energy spectrum presents regions where the density of the states is higher. These regions are equally spaced and are called Landau levels, which represent the quantization of the cyclotron orbits of charged particles.

These examples are made qmsolve, an open-source python open-source package we made for visualizing and solving the Schrödinger equation, with which we recently added an efficient time-dependent solver!

You can find the simulator used here:

This particular example was solved using the Crank-Nicolson method with a Cayley expansion, parallelized on GPU with cupy.

#SchrödingerEquation #QuantumPhysics #QMsolve

[metacarpo]

Wow, I've just found your channel and I'm absolutelly in love with it.
Im developing a kinda weird particles simulatior myself, classical not quantum, just for fun pourposes and maybe share with students, but now I wanna try this QM as well. Again, nice!

[justinpyle]

Great channel; Cant beleive i didnt find it sooner. i will be watching all your videos in order.
I wish more people would be interested in this type of video.

[streamofconsciousness]

Do you think he would have had a vague idea of what this looked like from the Maths on a chalk board kind of like a Musician looking at a score having a basic idea of the piece.

[carrotwine]

This looks fantastic. So fantastic, i need to ask: how long this kind of simulations take to compute(and what's the hardware, of course)? Is it hard to parallelize it on GPU, with basic knowledge of python?
Anyway, this really looks very fresh even for a guy who has seen a lot of simulations. I really like your visualization of wave function - not too much color, looks a bit like chromatic abberation, very cool. And the way it weirdly warps comes close to reignite my passion for math through physics:)

[DavideCernuzio]

Nice job! Is there a way to solve the eigenvalues' problem form this kind of hamiltonian? Or did you solve it in a numerical way? Thank you!

[exonysis]

Can I use these videos I give you Credit too

[BloodlinesNewTimes]

Is that like a 4d tube semi 3d {illusion|allusion of it}

[SafetySkull]

Could you please do a free electron encountering a coulomb potential?

[coolman]

Hi there, I'm currently looking for a project to do in matlab. I was wondering if you wrote the qmsolve library? I'm looking to solve the 1D and 2D time dependent shrodinger equation. What methods did you use to do so?

[scur_]

The typa gadgets the machine elves be showin ya.

[azharmalik]

Which software you use for these type of simulations kindly inform me because my final year project is also on quantum simulations so give me information about this phenomena