filmov
tv
Linear Algebra 2e: Confirming All the 'Tivities

Показать описание
Linear Algebra 2e: Confirming All the 'Tivities
Linear Algebra 2e: Confirming All the 'Tivities
Linear transformations | Matrix transformations | Linear Algebra | Khan Academy
Gilbert Strang: Linear Algebra vs Calculus
Example of finding (and proving) the existence of a basis: Linear algebra II
How to Find the Matrix of a Linear Transformation
Linear Transformations , Example 1, Part 1 of 2
One-to-one, Onto, and the Big Theorem Part II
Revision | Week-11 and 12
Linear Algebra Example Problems - Linear Combination of Vectors #2
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Linear combinations, span, and basis vectors | Chapter 2, Essence of linear algebra
When mathematicians get bored (ep1)
The Vector Space of Polynomials: Span, Linear Independence, and Basis
linear algebra vector space (25 examples)
How REAL Men Integrate Functions
Trying transition video for the first time 💙😂 || #transformation #transition #shorts #viralvideo...
Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school
Linear Algebra: help session, post-mortem of Test 2, e-vector example, 4-5-18, part 1
How to Prove a Set is a Subspace of a Vector Space
How to find out if a set of vectors are linearly independent? An example.
Logical Reasoning???#viral #vidumzn
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
Before JEE vs After JEE 😍 | My Transformation💔 | IIT Motivation|Jee 2023 #transformation #iit #viral...
Комментарии
 0:12:53
0:12:53
 0:15:08
0:15:08
 0:13:52
0:13:52
 0:02:14
0:02:14
 0:28:51
0:28:51
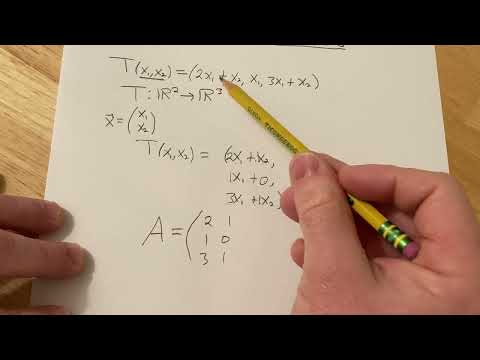 0:05:19
0:05:19
 0:09:06
0:09:06
 0:09:30
0:09:30
 2:28:16
2:28:16
 0:03:53
0:03:53
 0:10:59
0:10:59
 0:09:59
0:09:59
 0:00:37
0:00:37
 0:12:50
0:12:50
 0:30:16
0:30:16
 0:00:35
0:00:35
 0:00:15
0:00:15
 0:00:15
0:00:15
 0:59:51
0:59:51
 0:05:58
0:05:58
 0:04:41
0:04:41
 0:00:11
0:00:11
 0:00:16
0:00:16
 0:00:20
0:00:20