filmov
tv
the end-of-year exponential equation!
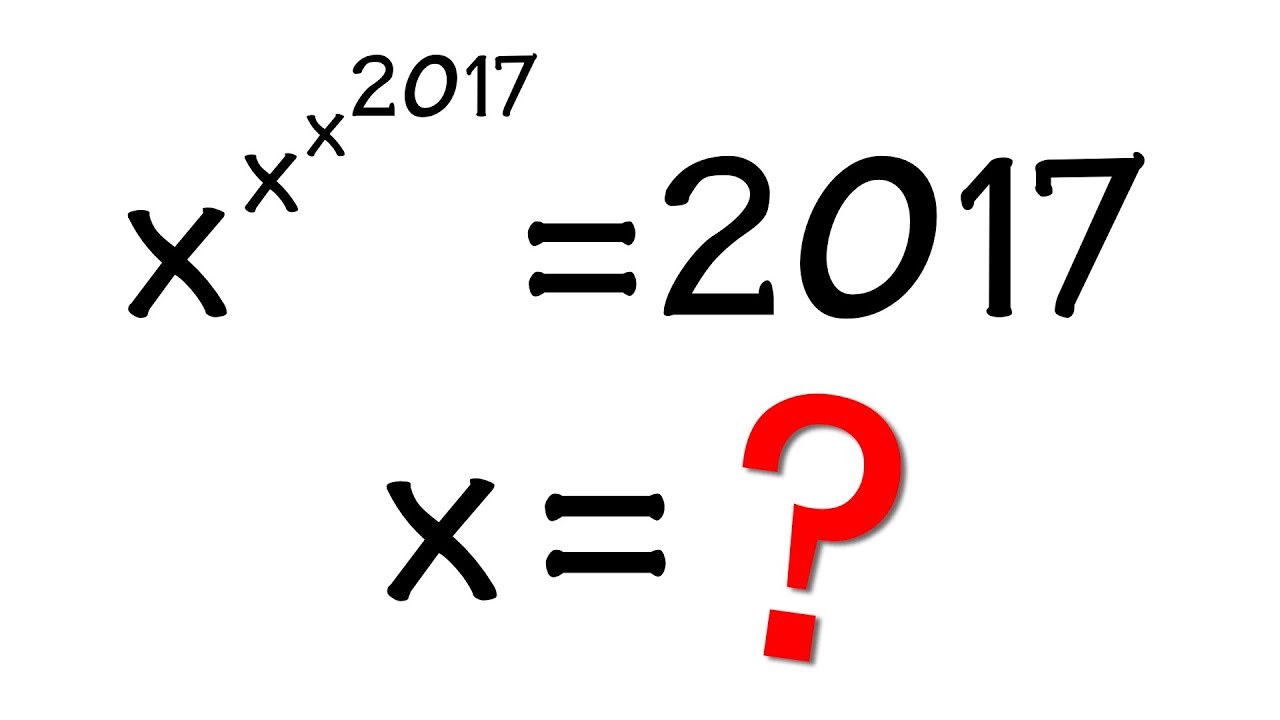
Показать описание
the end-of-year exponential equation!
Exponential Equations - Algebra and Precalculus
Tips on Solving an Exponential Equation
mystery exponential equation (alternative ending)
A Nice Algebra Problem | Math Olympiad | A Tricky Exponential Equation
Can you solve this? | Exponential Equation | Algebra Problem.
Nice Exponential equation | use this trick to solve exponential equation | math Olympiad training
A Nice Exponential Equation Celebrating the Year of 2023
AP Precalculus Practice Test: Unit 2 (35 Multiple Choice and 4 Free Response Questions)
Solving an Interesting Exponential Equation with Special Skill - Math Olympiad
Solving A Quick and Easy Exponential Equation
Exam Exponential Equations Grade 9
Exponential Equation Grade 10
Grade 11 Equations Exam Questions | Exponential Equations
A Surprising Exponential Equation
What is log 0 =? #shorts #logs #logarithm #math #maths #logarithms #explore #brazillian
Evaluating and Graphing Exponential Functions
How to Graph Exponential Functions
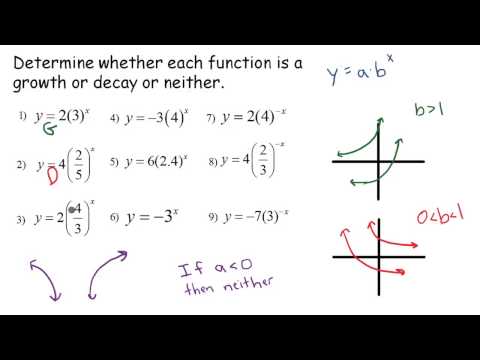
Exponentials: Determine if the exponential function is a growth, decay, or neither.
Exponential functions got you stumped? 😭 Here's how to solve them step by step!
Can you solve this tricky exponential equation?
Solving A Quick and Easy Exponential Equation
A Radical Exponential Equation | Bonus at the End
LAWS OF EXPONENTS | MATHS TRICKS
Комментарии
 0:08:38
0:08:38
 0:05:58
0:05:58
 0:00:48
0:00:48
 0:01:26
0:01:26
 0:08:08
0:08:08
 0:03:33
0:03:33
 0:04:44
0:04:44
 0:05:24
0:05:24
 1:29:33
1:29:33
 0:07:04
0:07:04
 0:00:28
0:00:28
 0:04:34
0:04:34
 0:01:39
0:01:39
 0:08:07
0:08:07
 0:08:51
0:08:51
 0:00:09
0:00:09
 0:05:59
0:05:59
 0:00:40
0:00:40
 0:03:22
0:03:22
 0:00:54
0:00:54
 0:11:12
0:11:12
 0:00:28
0:00:28
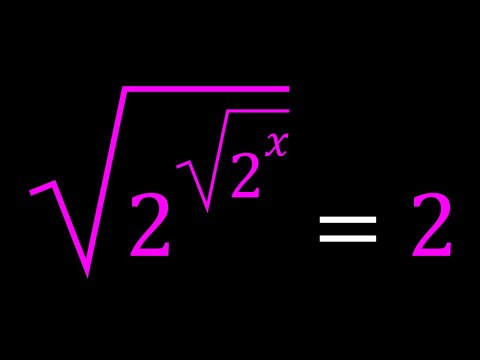 0:05:05
0:05:05
 0:00:42
0:00:42