filmov
tv
derivative of tetration of x (hyperpower)
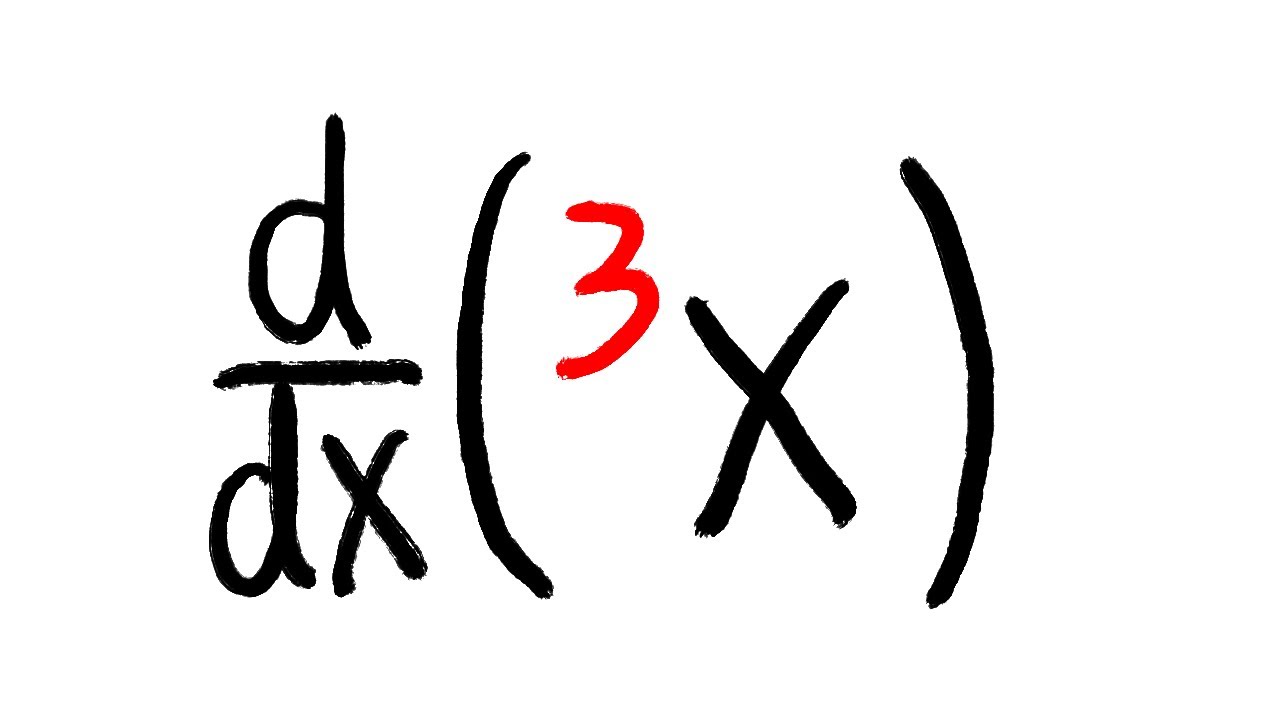
Показать описание
Derivative of tetration of x, derivative of (x↑↑3), derivative of double up arrows, derivative of tetration of x, Knuth Arrow Notation. This is a hard calculus 1 problem when we differentiate this power tower of x
#blackpenredpen #calculus #math #tutorial #college
#blackpenredpen #calculus #math #tutorial #college
derivative of tetration of x (hyperpower)
Derivative of the 6th tetration of x
Derivative of the 5th tetration of x
Is there a nice closed form for this tetration derivative?
Derivation of n-th tetration of x
Derivatives of x^x and x^x^x (2nd and 3rd tetrations of x)
how to prove the derivative of the nth tetration of x
Derivative of the 4th tetration of x
Derivative of x^x^x... infinite tetration
what is the infinite tetration of i
Every Student Should See This
Convergent Infinite tetration
How REAL Men Integrate Functions
Have You Heard of Tetration, Pentation, and Hexation? #shorts
Differentiate x^x^x^x
When mathematicians get bored (ep1)
How to differentiate tetration!
5 simple unsolvable equations
y =x^x; Find dy/dx | Derivative of Tetration Function | Calculus
A 'tetration with infinite height' integral
Differentiation of Tetration Functions : How to differentiate Tetration Functions #excellenceacademy
Derivative of tetration of x ( hyperpower) by gd sir
solving the tetration equation x^x^x=2 by using Newton's Method
I Couldn't Find this Derivative
Комментарии
 0:10:58
0:10:58
 0:05:52
0:05:52
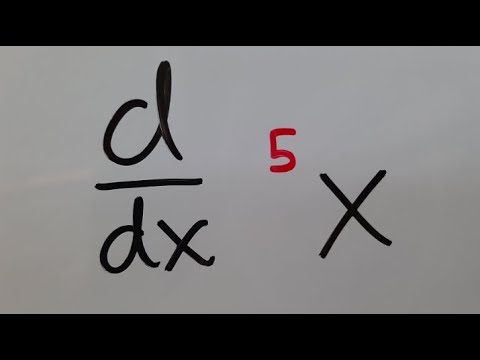 0:07:28
0:07:28
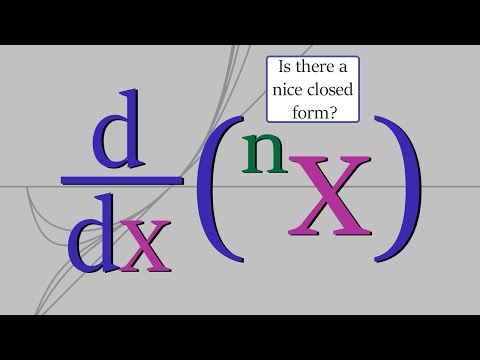 0:16:50
0:16:50
 0:16:22
0:16:22
 0:09:11
0:09:11
 0:15:11
0:15:11
 0:12:14
0:12:14
 0:12:25
0:12:25
 0:04:36
0:04:36
 0:00:58
0:00:58
 0:17:26
0:17:26
 0:00:35
0:00:35
 0:00:27
0:00:27
 0:16:28
0:16:28
 0:00:37
0:00:37
 0:26:08
0:26:08
 0:00:50
0:00:50
 0:03:47
0:03:47
 0:19:37
0:19:37
 0:10:58
0:10:58
 0:03:56
0:03:56
 0:07:02
0:07:02
 0:03:58
0:03:58