filmov
tv
Without integration, why is the volume of a paraboloid half of its inscribing cylinder? (DIw/oI #8)

Показать описание
Rather than using integration, can we find the volume of a paraboloid? Yes, if we accept a precursor to calculus - Cavalieri's principle. Usually, integration is needed to find the volume of a paraboloid, for example using shell method, but using Cavalieri's principle, and a sneaky little trick, we can find the volume very easily - half of the volume of the circumscribing cylinder!
The idea for this video isn't actually mine, but thanks to Yehuda Simcha Waldman for suggesting the idea of this video! He emailed me about the proof, and I modified it a little bit and adapted it into this video that you are watching here.
Other than commenting on the video, you are very welcome to fill in a Google form linked below, which helps me make better videos by catering for your math levels:
If you want to know more interesting Mathematics, stay tuned for the next video!
SUBSCRIBE and see you in the next video!
If you are wondering how I made all these videos, even though it is stylistically similar to 3Blue1Brown, I don't use his animation engine Manim, but I will probably reveal how I did it in a potential subscriber milestone, so do subscribe!
Social media:
For my contact email, check my About page on a PC.
See you next time!
The idea for this video isn't actually mine, but thanks to Yehuda Simcha Waldman for suggesting the idea of this video! He emailed me about the proof, and I modified it a little bit and adapted it into this video that you are watching here.
Other than commenting on the video, you are very welcome to fill in a Google form linked below, which helps me make better videos by catering for your math levels:
If you want to know more interesting Mathematics, stay tuned for the next video!
SUBSCRIBE and see you in the next video!
If you are wondering how I made all these videos, even though it is stylistically similar to 3Blue1Brown, I don't use his animation engine Manim, but I will probably reveal how I did it in a potential subscriber milestone, so do subscribe!
Social media:
For my contact email, check my About page on a PC.
See you next time!
Комментарии
 0:04:39
0:04:39
 0:07:49
0:07:49
 0:05:46
0:05:46
 0:00:09
0:00:09
 0:00:33
0:00:33
 0:04:36
0:04:36
 0:02:32
0:02:32
 0:06:01
0:06:01
 0:00:32
0:00:32
 0:14:54
0:14:54
 0:22:40
0:22:40
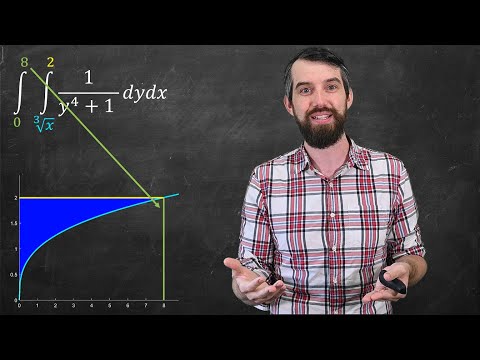 0:07:39
0:07:39
 0:00:59
0:00:59
 0:00:16
0:00:16
 0:07:04
0:07:04
 0:10:57
0:10:57
 0:00:10
0:00:10
 0:00:41
0:00:41
 0:00:59
0:00:59
 0:22:56
0:22:56
 0:00:25
0:00:25
 0:00:47
0:00:47
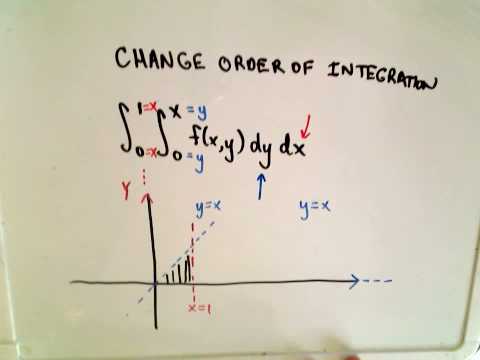 0:04:20
0:04:20
 0:00:46
0:00:46