filmov
tv
Can you change a sum by rearranging its numbers? --- The Riemann Series Theorem

Показать описание
Normally when you add up numbers, the order you do so doesn't matter and you get the same sum regardless. And, of course, the same holds true even if you add up infinitely many numbers.....
Right?
=Chapters=
0:00 - Let's rearrange a sum!
1:48 - Investigation
6:32 - Riemann Series Theorem explained visually
13:58 - Resolving objections
18:52 - A step further and a challenge
20:07 - Significance of the Riemann Series Theorem
21:47 - Final thoughts
This video is a participant in the 3Blue1Brown First Summer of Math Exposition (SoME1). You can find out more about it here:
#SoME1
===============================
Thank you for your support!
===============================
The animations in this video were mostly made with a homemade Python library called "Morpho".
If you want to play with it, you can find it here:
Right?
=Chapters=
0:00 - Let's rearrange a sum!
1:48 - Investigation
6:32 - Riemann Series Theorem explained visually
13:58 - Resolving objections
18:52 - A step further and a challenge
20:07 - Significance of the Riemann Series Theorem
21:47 - Final thoughts
This video is a participant in the 3Blue1Brown First Summer of Math Exposition (SoME1). You can find out more about it here:
#SoME1
===============================
Thank you for your support!
===============================
The animations in this video were mostly made with a homemade Python library called "Morpho".
If you want to play with it, you can find it here:
Can you change a sum by rearranging its numbers? --- The Riemann Series Theorem
Sum 41 - Subject to Change (lyrics)
can you find the trick for this infinite sum??
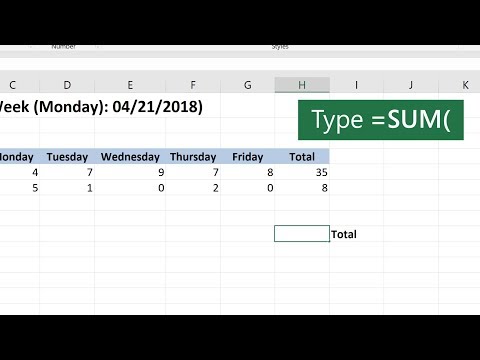
SUM Formula in Excel | Add Total Values #shorts #excel
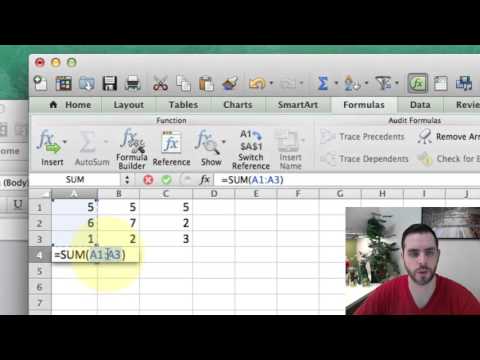
How to use the SUM function in Microsoft Excel
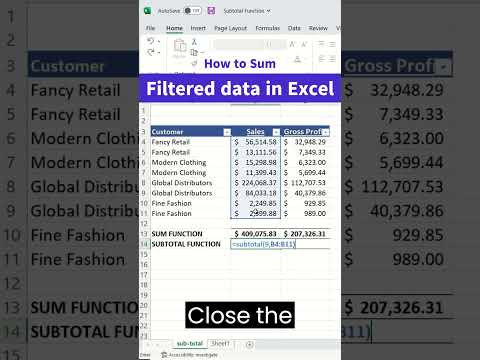
How to sum filtered data in Excel
Sum 41 - Subject To Change [Chuck (Japanese Edition)]
How to Sum a Column or Row of Excel Cells
AP calculus AB | College Board | FRQ 2024 solutions
Why Sum Function Returns 0 in Excel
Excel not formatting cell contents as numbers, won't sum cells -decimal separator - comma and p...
What is the sum of 3/4 and 2/3?
#Shorts - AutoSum Formula in Word | How to Sum in Word
Excel Pivot Table: How to change Count to Sum
Using Sum Formulas and Change of Index
Excel Trick to Sum Values separated with commas
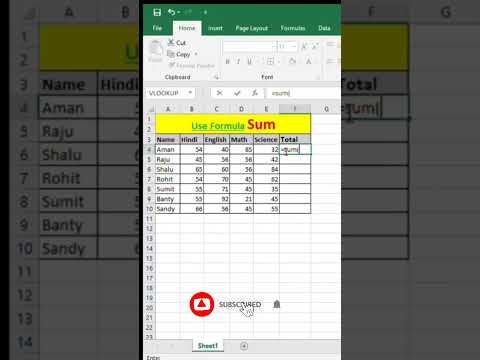
Use Sum Formula In Excel | Excel Sum Formula In Hindi
Add numbers in columns in a Word table: Insert formula to sum a column or row of table in Word?
Sum 41 - Subject to Change *HQ sound*
Excel - How to Make a Sum Negative in Excel #shorts #exceltricks - Episode S0010
How to Sum Cells by Color in Excel (Get it to update automatically)
Excel: Sum Across Multiple Columns With One or More Criteria - 3 Methods
Excel - Why Excel SUM is Zero #Shorts #microsoftexcel #excel - Episode S0003
Don't use =Sum in Excel #shorts
Комментарии
 0:23:48
0:23:48
 0:03:17
0:03:17
 0:10:27
0:10:27
 0:00:10
0:00:10
 0:00:38
0:00:38
 0:00:32
0:00:32
 0:03:16
0:03:16
 0:01:02
0:01:02
 2:30:37
2:30:37
 0:01:08
0:01:08
 0:02:40
0:02:40
 0:03:05
0:03:05
 0:00:12
0:00:12
 0:01:29
0:01:29
 0:09:47
0:09:47
 0:03:13
0:03:13
 0:00:06
0:00:06
 0:00:34
0:00:34
 0:03:17
0:03:17
 0:00:29
0:00:29
 0:10:54
0:10:54
 0:04:53
0:04:53
 0:01:00
0:01:00
 0:00:22
0:00:22