filmov
tv
China Math Olympiad | A Nice Geometry Problem | 2 Methods
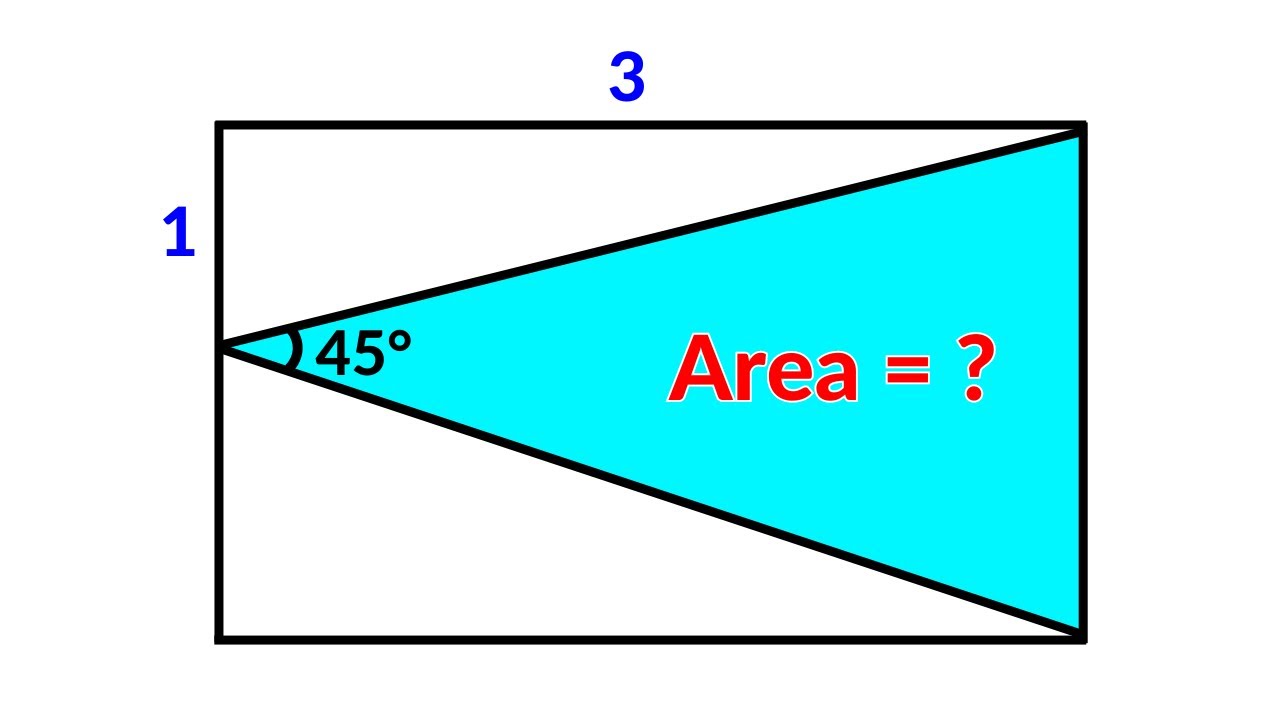
Показать описание
China Math Olympiad | A Nice Geometry Problem | 2 Methods
MY OTHER CHANNELS
••••••••••••••••••••••••••••••••
--------------------------------------------------------------------------------
Join the channel to become a member
MY OTHER CHANNELS
••••••••••••••••••••••••••••••••
--------------------------------------------------------------------------------
Join the channel to become a member
Chinese IMO team
How to win the International Math Olympiad | Po-Shen Loh and Lex Fridman
China | Math Olympiad | A Nice Algebra Problem 👇
China Math Olympiad | A Very Nice Geometry Problem | 2 Different Methods
Chinese Math Olympiad Problem | A Very Nice Geometry Challenge
China Math Olympiad | You should be able to solve this | 2 Methods
A Chinese Math Olympiad Question | You should know this trick!
China Math Olympiad | A Nice Geometry Problem | 2 Methods
'I study mathematics using my heart'
Top 20 Country by International Mathematical Olympiad Gold Medal (1959-2019)
Viral question from China
China Math Olympiad | A Very Nice Geometry Problem
Students 'speed-read' at competition in China
China Math Olympiad | A Very Nice Geometry Problem | 2 Methods
China Math Olympiad Problem | A Very Nice Geometry Challenge | 4 Different Methods
Team USA wins Math Olympiad: US beats China for first time in 20 years - TomoNews
China | Math Olympiad | Nice Algebra Problem 👇
China | A Very Nice Algebra Problem | Math Olympiad
Tips from the coach of China’s International Mathematical Olympiad team
Chinese Junior Math Olympiad Problem
USA Math Teams Olympiad really beats China? | More video at Video Lisation
Chinese Math Olympiad Question | A Nice Trignometry Equation Solving
China Math Olympiad | A Very Nice Geometry Problem
China | Math Olympiad | A Nice Algebra Problem 👇👇👇
Комментарии
 0:00:34
0:00:34
 0:04:00
0:04:00
 0:10:37
0:10:37
 0:18:02
0:18:02
 0:12:31
0:12:31
 0:13:35
0:13:35
 0:03:20
0:03:20
 0:14:32
0:14:32
 0:00:40
0:00:40
 0:02:21
0:02:21
 0:08:04
0:08:04
 0:09:10
0:09:10
 0:01:16
0:01:16
 0:18:01
0:18:01
 0:28:01
0:28:01
 0:01:42
0:01:42
 0:07:02
0:07:02
 0:10:20
0:10:20
 0:00:45
0:00:45
 0:03:31
0:03:31
 0:00:29
0:00:29
 0:12:55
0:12:55
 0:13:51
0:13:51
 0:11:57
0:11:57