Reflection about y = 2x

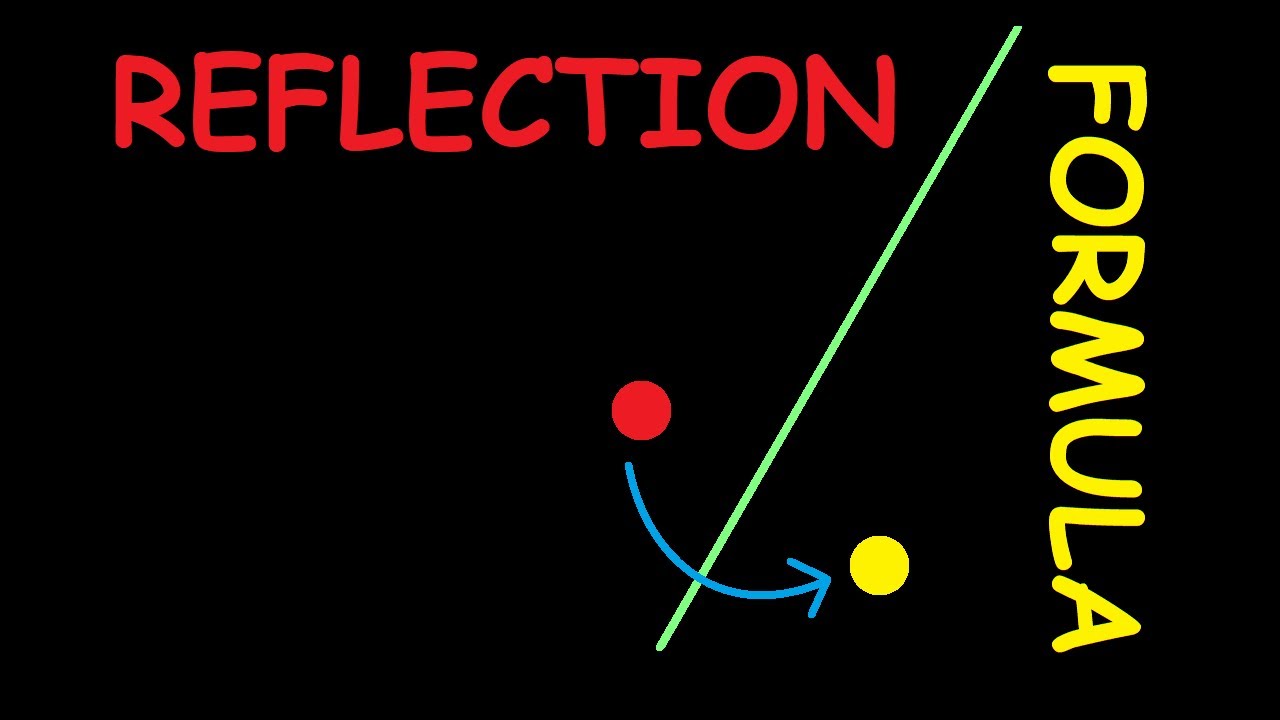
Formula of reflection about the line y = 2x

In this video, I present a really neat application of change of coordinates: Namely, I calculate the formula of the reflection of a point about the line y = 2x. Can you guess the formula beforehand? You might be surprised! Enjoy

[guyguy]

I asked my teacher about this and she said it wasn't possible. Gonna annoy her tomorrow 😂😂

[eliyasne]

I did not use linear algebra.
Me solution uses complex numbers.
Here it is:
In order to find a mapping transformation for a mirror placed on y=2x i started by making a point in the complex plane such that its angel with the "real" number line is that of the line y=2x and its magnetude is one. Then i made a second, general point that the transformation would act onto. Now, my transformation is the following: to get the output point i multiply the input point by the square of the ratio
((special point)/(input point divided by its magnitude))
In the end i can take the general coordinates of my output complex number and they would be the answer.

[blackpenredpen]

Yo thumbnail is on point again, Dr. P!! Love it!

[fredhasopinions]

This is such a fun video! Exactly what I needed for my assignment BUT also explained in such an enthusiastic way. Thank you for this.

[thedoublehelix]

Woah! I used linear algebra on a school assignment once. The final for my precal class was to draw a picture using graphs. I used linear transformations to rotate functions to what I wanted. I also used calculus to come up with really accurate features. (What I did was plot the points I wanted to connect with my equation, then found the slope between the points and created a derivative graph. Then used regression and integration to smooth things out)

[yoavshati]

You could easily do it for any linear equation y=mx+n and a point P(a, b) by finding the perpendicular line to the linear function that also passes through the point, which will be y=((a-x)/m)+b, and then you can find the intersection, which is the midpoint of P and P', so you can find P'

[victoroa]

Dr Peyam! Two days ago I just had an important exam which had an exercise about this. If only you would have uploaded this video earlier 😢

[pizzacat]

If only I had watched this video yesterday...

[ArtelValenheart]

I've found the same matrix by simply solving a system of equations { T(1, 2) = (1, 2), A(-2, 1) = (2, 1) }, where T is a linear operator with matrix { { a, b }, { c, d } } in Cartesian coordinate system.

[fantiscious]

Not completely related to the video, but I found a function that describes part of the graph e^x flipped across y = 2x. It has the Lambert W function in it, here it is

[For x>0.7726, y<0.2198]: F(x) = -4x/3 + 2W(-4/3 * e^[-5x/3]) - 1/2 * W(2 * e^[-5x/3 - 5/2 * W(-4/3 * e^[-5x/3])])


It has an exponent INSIDE of an exponent so I'm not sure if anything can be simplified or not :v

[franchello]

You could get the same results with 3 simple tranformations? Rotation[[cos(tan^-1(.5)), sin(tan^-1(.5))], [-sin(tan^-1(.5)), cos(tan^-1(.5))] Reflection[[-1, 0], [0, 1]] Rotation[[cos(-tan^-1(.5)), sin(-tan^-1(.5))], [-cos(-tan^-1(.5)), sin(-tan^-1(.5))]]

Rotate your axis of reflection so that it becomes the y axis, reflect around the y-axis, then rotate back.

[bryanwright]

easy to do without linear algebra. For example reflect the point (6, 3) about line y = 2x
step one: calculate equation of line with (6, 3) that is perpendicular to y = 2x
it is y = -1/2 x + 6
step two: use systems of equations to solve for point of intersection which is (12/5, 24/5)
third: since this is midpoint the reflected point easy to solve for (-6/5, 33/5)
Lot easier!

[MrRyanroberson]

Reflect about the line x sin(t) = y cos(t):
if we rotate the plane such that the line meets the x axis, then negate, then rotate back, it should work. so let's take the formula: e^-it * [1, 0;0, -1] * e^it, e^it being a rotation matrix. The first two multiply to give [cos, sin;sin, -cos], and multiplying that by e^it gives [cos^2-sin^2, 2sincos; 2sincos, sin^2-cos^2] which if i recall is equivalent to the quaternion (cos^2-sin^2)i + (2sincos)k = (1-2sin^2)i + (2sincos)k for any angle input to the sines and cosines. Odd how this is supposed to map from 2d to 2d... is it really guaranteed that this quaternion works?

[thesakinator]

Why not just solve the system of equations using the known points @4:36 ? You have a + 2b = 1 and c + 2d = 2, as well as -2a + b = 2 and -2c + d = -1. This easily becomes 5b = 4 and b = 4/5, and then a = -3/5, and similarly 5d = 3 and d = 3/5, c = 4/5

[shiina_mahiru_]

T is much nicer if you use y=(tanθ)x instead of y=mx

[Okiel]

I had this question days ago with flipping over diffrent equations other than y = x high-school junior math class, and it gave me a headache so basically shrugged it off to just being to advanced for me mostly bc i thought it had to do with trigonometry. Now I want to make a 3d rendering of a cube I can rotate in pygame and it led me to this😅

[alexhernandez]

The truth I love your videos I am your fan and I would like you to share more math topics that this matery I love I sleep two hours to study it, to be a great mathematician like you and I would like you to share topics, only basic topics like theorem of pick and others I hope you share more topics: '(

[non-inertialobserver]

I did this without linear algebra, and was honestly quite easy, but the linear algebra way is very elegant :)

[benjaminbrady]

The Linear Algebra in this is too hard for me :/
Is there a recommendation of where to learn this?

[gordonchan]

I think finding the reflection about y = mx + c with algebra only is not too difficult.