filmov
tv
Projection on y = 2x

Показать описание
Projection on line y = 2x
In this video, as a sequel to my reflection video, I calculate the formula of the reflection of a point about the line y = 2x. Of course one can do it more easily using multivariable calculus, but this is meant to be an application of change of coordinates, to illustrate the power of linear algebra. Enjoy!
In this video, as a sequel to my reflection video, I calculate the formula of the reflection of a point about the line y = 2x. Of course one can do it more easily using multivariable calculus, but this is meant to be an application of change of coordinates, to illustrate the power of linear algebra. Enjoy!
Projection on y = 2x
Linear Algebra: Projection onto a Line
2.1 Matrices Intro - #06 Linear Transformation Example (Projection to Line y=mx)
Linear Transformations Projection of X and Y Axis Using 2x2 Matrix
Orthogonal Projection onto a Line - Coffee and Linear Algebra with Dr. Weselcouch
How to Find the Matrix of a Linear Transformation
Matrices Quick Tip for Rotating and Reflecting
Concept Check: Describe the Kernel of a Linear Transformation (Projection onto y=x)
Projection Matrix 2
Perspective projection in 5 minutes: Part 2 -- the math!
416.1B Projection and an Overspecified Linear System
Geometric transformations: projection onto a line
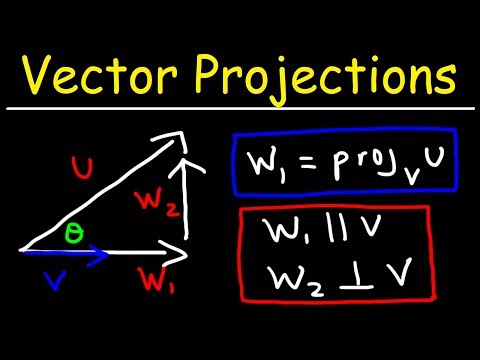
Calculus 3 - Vector Projections & Orthogonal Components
Math 2.5.3: Projection as linear transformation
Orthogonal projection to subspace
Matrix Transformations : reflections and rotations
Finding the projection of a line on a plane
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
How REAL Men Integrate Functions
Matrix Transformation: Projection onto the xy-plane
Line of reflection example
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Sine Curve and the Unit Circle
Projection concept formulas and solved example
Комментарии
 0:10:08
0:10:08
 0:09:14
0:09:14
 0:13:37
0:13:37
 0:30:57
0:30:57
 0:02:53
0:02:53
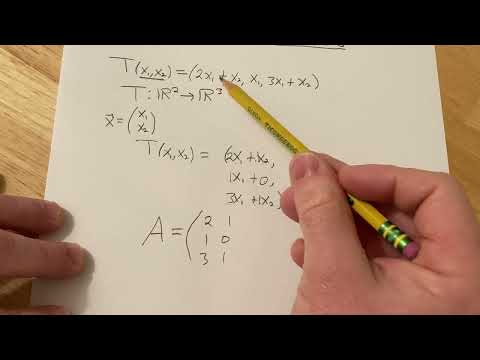 0:05:19
0:05:19
 0:03:11
0:03:11
 0:02:50
0:02:50
 0:10:38
0:10:38
 0:04:24
0:04:24
 0:17:56
0:17:56
 0:26:47
0:26:47
 0:12:14
0:12:14
 0:03:53
0:03:53
 0:06:03
0:06:03
 0:03:26
0:03:26
 0:10:36
0:10:36
 0:00:16
0:00:16
 0:00:35
0:00:35
 0:02:39
0:02:39
 0:01:40
0:01:40
 0:10:59
0:10:59
 0:00:27
0:00:27
 0:11:13
0:11:13