Coordinate Transformations in 2D (Part 2) | Mapping | Robotics 101

In this video, we discuss the general case of coordinate transformations consisting of both rotation & translation combined.

The mathematics behind it is also shown in the light of robotics and I have included an example along the way.

🌟 Contents 🌟
00:00 General coordinate transformation
02:10 Special cases of coordinate transformation
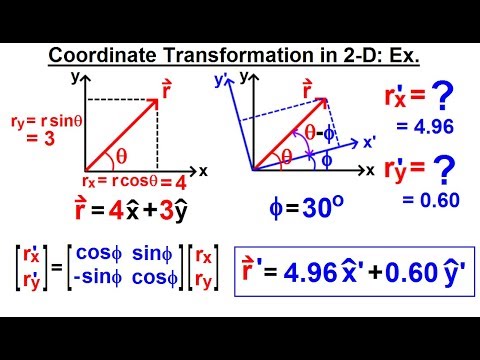
03:06 Example of changing frames (moving from fixed frame to moving frame)

In the next couple of videos, we take it a step further and apply coordinate transformations to 2D robots to see how it enables us to change the representation of an object from a body frame to a fixed frame (and vice versa).

------

This video is part of the Robotics 101 tutorial series which covers kinematics and modeling of 2D & 3D robots.

This tutorial lesson series starts from the basics of robotics (assuming no prior knowledge) and gradually builds on in bite-sized videos of 10 minutes or less. By following along, you will soon become extremely good in the kinematics and modeling aspects of robots. And these will help you to design and build robots.

Here's what we will cover in this video series:
1. Co-ordinate Transformation for 2D & 3D robots
2. Homogeneous Transformations for 2D & 3D robots
3. Forward Kinematics
4. Inverse Kinematics
5. Robotic wrists (end-effector)
6. End-effector Velocities and Jacobians
7. Singularities of robots
8. Gimbal Locks
9. Forces & Torques

I will be uploading 1 video per week. If you find these helpful, don't forget to share and subscribe!

_____________________________
👉 Link to the Robotics 101 playlist

Robotics 101 - Robotics full course for beginners - Kinematics and Modeling

#roboticsforbeginners #roboticsTutorials #robotics #learnrobotics#homogenoustransformationmatrices #configuration #rotationmatrix #mechatronics #orientation #orientationinrobotics #transformationmatrices #displacementinrobotics #poseinrobotics #pose #translationandrotation

[EngineeringSimplified]

✍Any Questions, doubts, or thoughts? Comment below (I read & respond to every comment).
👉Don't forget to SUBSCRIBE to the channel for more such videos & courses: bit.ly/Engineering-Simplified

[Qurqud]

I think we rotate small x first and then move it by vector d, as your formula shows we first rotate it first and then transfer it by vector d.
I think if we move the coordinate system first and then rotate it then we will have
X = A( d+ x)

[jamiejames]

Hello, thanks for the video. However, at 01:50 I really don't understand how (vector X) = A*(vector x)+(vector d)
when vector x is a vector that is already rotated. Why do we rotate vector x again by matrix A?

[jayrana]

Please make similar playlist on dynamics and control of robotics as well.. 🙏

[mr.perfect]

Can we calculate this by using homogeneous transform?