filmov
tv
Math Olympiad Question | A Nice Algebra Problem | What Is The Value Of 'X' In This Equation?
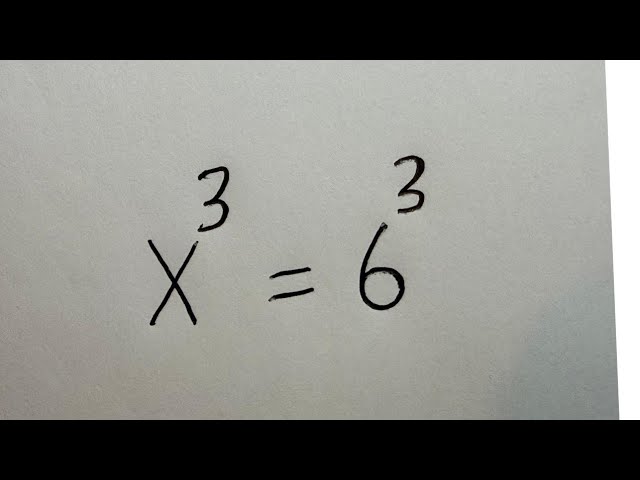
Показать описание
Hello 👩❤️👨👩❤️👨👩❤️👨
How Are You Today👍👍👍
If you like this video about
How To Solve This Nice Math Olympiad Algebra Problem,
Please Like And Subscribe To My Channel 🙏🙏🙏
#matholympiad #algebra #olympiadmathematics #mathsfocus #statistics #maths #MathOlympiadPrep #AlgebraSolutions #ExponentialFunctions #MathForKids #AlgebraMadeEasy #MathOlympiadQuestions #ExponentialEquations #MathTutoring #MathPractice #AdvancedMath #MathsFocus #MathOlympiad #Algebra #ExponentialProblems #MathChallenge #MathTips #MathTricks #MathCompetition #LearnMath #MathSkills #MathOlympiadPrep #AlgebraSolutions #ExponentialFunctions #MathForKids #AlgebraMadeEasy #MathOlympiadQuestions #ExponentialEquations #MathTutoring #MathPractice #advancedmaths
Thank You
How Are You Today👍👍👍
If you like this video about
How To Solve This Nice Math Olympiad Algebra Problem,
Please Like And Subscribe To My Channel 🙏🙏🙏
#matholympiad #algebra #olympiadmathematics #mathsfocus #statistics #maths #MathOlympiadPrep #AlgebraSolutions #ExponentialFunctions #MathForKids #AlgebraMadeEasy #MathOlympiadQuestions #ExponentialEquations #MathTutoring #MathPractice #AdvancedMath #MathsFocus #MathOlympiad #Algebra #ExponentialProblems #MathChallenge #MathTips #MathTricks #MathCompetition #LearnMath #MathSkills #MathOlympiadPrep #AlgebraSolutions #ExponentialFunctions #MathForKids #AlgebraMadeEasy #MathOlympiadQuestions #ExponentialEquations #MathTutoring #MathPractice #advancedmaths
Thank You
Math Olympiad Question | You should know this trick!!
Maths Olympiad | A Tricky Exponential Equation - Be Careful
Math Olympiad Question
The unexpectedly hard windmill question (2011 IMO, Q2)
A Nice Math Olympiad Exponential Equation 3^x = X^9
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Norway Math Olympiad Question | You should be able to solve this!
Luxembourg - Math Olympiad Question | You should know this trick
IMO ~ Maths Olympiad | Class - 2 | Worksheet ~ 10 | 20 Questions | By- Sudhir Sir
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
Solving an IMO Problem in 6 Minutes!! | International Mathematical Olympiad 1979 Problem 1
2017 Raytheon MATHCOUNTS National Competition
Thailand | Math Olympiad Question | Nice Algebra Equation
New Zealand - Math olympiad Question
Germany - Math Olympiad Question
Maths Olympiad | A Tricky Maths Olympiad Questions | Algebra Problem |
Nice Math Olympiad Algebra Equation | How to Solve?
Maths Olympiad | A Tricky maths olympiad question | Algebra problems |
Math Olympiad 3^m–2^m=65 | Math Olympiad Problems | Algebra
France - Math Olympiad Question | An Algebraic Expression | You should be able to solve this!
Germany - Math Olympiad Question | The BEST Trick
।। maths olympiad question ।। An algebraic exponential problem @mathscuriosity494
Math Olympiad question | Trending shorts || #shorts #youtubeshorts #short
The Legend of Question Six - Numberphile
Комментарии
 0:00:33
0:00:33
 0:11:47
0:11:47
 0:08:35
0:08:35
 0:16:03
0:16:03
 0:02:34
0:02:34
 0:00:52
0:00:52
 0:03:21
0:03:21
 0:02:51
0:02:51
 0:07:21
0:07:21
 0:01:54
0:01:54
 0:06:40
0:06:40
 0:56:01
0:56:01
 0:01:26
0:01:26
 0:01:12
0:01:12
 0:11:00
0:11:00
 0:08:03
0:08:03
 0:10:40
0:10:40
 0:05:48
0:05:48
 0:10:49
0:10:49
 0:08:40
0:08:40
 0:10:37
0:10:37
 0:13:59
0:13:59
 0:00:15
0:00:15
 0:08:45
0:08:45