Differential Equations: Orthogonal Trajectories: Example 1

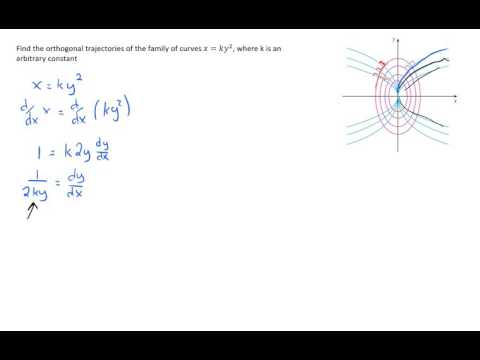
In this video I go over a recap on orthogonal trajectories as well as an example on how to go about solving for a family of orthogonal trajectories to the parabolas x = k*y^2, where k is a constant. The first step is to write the parabolas equation as a differential equation and solve for the derivative. Then, as proved in my earlier video, if a curve is perpendicular or orthogonal to another, then the slopes of the tangent line must be a negative reciprocal to the tangent line of the other curves. Thus from this fact we can obtain a second differential equation, which luckily is a separable equation, and can be solved resulting in a family of ellipses. This is a very useful example on the steps involved in determining the orthogonal trajectories, which are actually used a lot in physics and engineering applications such as electricity and fluid-dynamics!

Related Videos:

------------------------------------------------------

[mes]

I don't always determine the orthogonal trajectories of a family of curves but when I do I usually set up a differential equation and look at the negative reciprocal of the slope to form a second differential equation ;)

[jasmines]

Thankyou! This helped me a-lot with understanding the concept :D

[JacksonBucholz]

Hey quick question! Is it possible to solve these problems without setting up implicit differential equations? For instance, in the first example can we just solve for y...

y = sqrt(x/k)

y' = 1/2sqrt(xk)

y' (perpendicular) = and then solve < that line for our function? Also, can you clarify please why we have to get rid of k. What do you mean by "simultaneously valid for all values of k"?

Thanks so much!

[itsSHKR]

i believe its "or-thawgonal" .... not "ortha-gone-al".... :3

[KanoBoom]

Odd thing is in my textbook the solution is 2x^2+y^2=c^2 I’m not sure why