filmov
tv
Orthogonal Trajectories and Differential Equations - Calculus 2
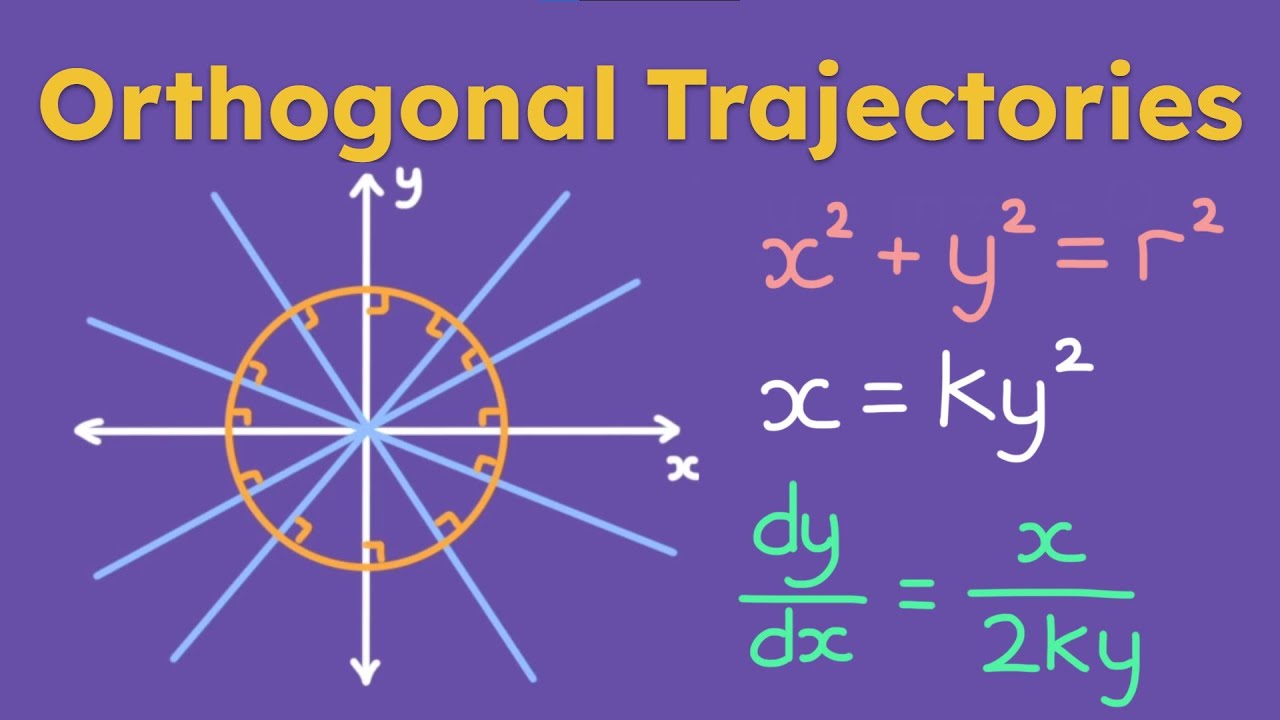
Показать описание
In this video, I will show you how to find the orthogonal trajectories using differential equations. This is a very important topic that students learn in Calculus 2. A differential equation is an equation with an unknown variable and its derivatives. Two trajectories are orthogonal to each other when their intersections form right angles. A simple example are two lines intersecting each other at a right angle, or a circle at the origin with a line passing through the origin and intersects the circle at a right angle. Orthogonal trajectories come up a lot in Physics classes. For example, in an electrostatic field, the lines of force are orthogonal to the lines of constant potential. Also, the streamlines in aerodynamics are orthogonal trajectories of the velocity-equipotential curves. To find the orthogonal slopes, simply take the negative reciprocal of the tangent equation of the family of curves. I go through many examples in the video. Usually, finding orthogonal trajectories will give you separable differential equations, which are easy to solve.
Orthogonal Trajectories and Differential Equations - Calculus 2
Orthogonal Trajectories - Differential Equations
Using separable differential equations to find orthogonal trajectories
Orthogonal Trajectories
Differential Equations: Orthogonal Trajectories: Example 1
DIFFERENTIAL EQUATIONS: ORTHOGONAL TRAJECTORIES TO y² = cx³
Applications of Differential Equations|Orthogonal Trajectories|Lecture 01|Engineering|B.Sc|Diploma
Orthogonal Trajectories, Application of First Order Differential Equations
IIT JAM 2025 | CUET PG | Mathematics | ODE | Higher Order Differential Equation | L 06 | Raman Sir
Finding Orthogonal Trajectories
Problem on Orthogonal Trajectory of Family of Curves / Problem-4
Orthogonal Trajectories
Orthogonal Trajectories - Differential Equation | Definition & Examples
ORTHOGONAL TRAJECTORIES | Application of First Order Differential Equation
Differential Equations: Orthogonal Trajectories
Differential Equations Applications - Orthogonal Trajectories
ORTHOGONAL TRAJECTORIES PART 1 DIFFERENTIAL EQUATION
Engineering Maths 1 orthogonal trajectory example (PART-1)
Orthogonal Trajectories | Differential Equations - Problems & solutions (Part 1)
Orthogonal Trajectories | Differential Equations
Orthogonal Trajectories | Differential Equations - Problems & solutions (Part 3)
Orthogonal trajectories - solved problem 1: Differential equations
mod05lec59 - Orthogonal Trajectories
Problem on Orthogonal trajectory of family of curves y^2=4ax/ Problem-3
Комментарии
 0:11:25
0:11:25
 0:04:25
0:04:25
 0:13:35
0:13:35
 0:05:40
0:05:40
 0:16:29
0:16:29
 0:06:26
0:06:26
 0:15:13
0:15:13
 0:14:53
0:14:53
 0:31:16
0:31:16
 0:09:26
0:09:26
 0:09:24
0:09:24
 0:09:18
0:09:18
 0:16:17
0:16:17
 0:13:00
0:13:00
 0:13:39
0:13:39
 0:09:56
0:09:56
 0:07:54
0:07:54
 0:04:44
0:04:44
 0:09:49
0:09:49
 0:38:32
0:38:32
 0:06:40
0:06:40
 0:06:11
0:06:11
 0:08:14
0:08:14
 0:04:59
0:04:59