filmov
tv
Quantum Chemistry 7.3 - Hydrogen Atom Radial Wavefunctions

Показать описание
Short lecture on hydrogen atom radial wavefunctions.
The wavefunctions of the hydrogen atom quantum mechanical model system can be separated into functions of the spherical polar coordinates r, theta, and phi. The functions of r are called the radial wavefunctions. The hydrogen radial wavefunctions are composed of a normalization constant, the associated Laguerre polynomials, and a decaying exponential of r. The inputs to each function depend on the quantum number n, l and m, as well as the Bohr radius a_o. The Laguerre polynomials can be produced from a generating formula or looked up in a table.
--- About TMP Chem ---
All TMP Chem content is free for everyone, everywhere, and created independently by Trent Parker.
--- Video Links ---
--- Social Links ---
--- Equipment ---
Microphone: Blue Yeti USB Microphone
Drawing Tablet: Wacom Intuos Pen and Touch Small
Drawing Program: Autodesk Sketchbook Express
Screen Capture: Corel Visual Studio Pro X8
The wavefunctions of the hydrogen atom quantum mechanical model system can be separated into functions of the spherical polar coordinates r, theta, and phi. The functions of r are called the radial wavefunctions. The hydrogen radial wavefunctions are composed of a normalization constant, the associated Laguerre polynomials, and a decaying exponential of r. The inputs to each function depend on the quantum number n, l and m, as well as the Bohr radius a_o. The Laguerre polynomials can be produced from a generating formula or looked up in a table.
--- About TMP Chem ---
All TMP Chem content is free for everyone, everywhere, and created independently by Trent Parker.
--- Video Links ---
--- Social Links ---
--- Equipment ---
Microphone: Blue Yeti USB Microphone
Drawing Tablet: Wacom Intuos Pen and Touch Small
Drawing Program: Autodesk Sketchbook Express
Screen Capture: Corel Visual Studio Pro X8
Quantum Chemistry 7.1 - Hydrogen Atom Model
Bohr Model of the Hydrogen Atom, Electron Transitions, Atomic Energy Levels, Lyman & Balmer Seri...
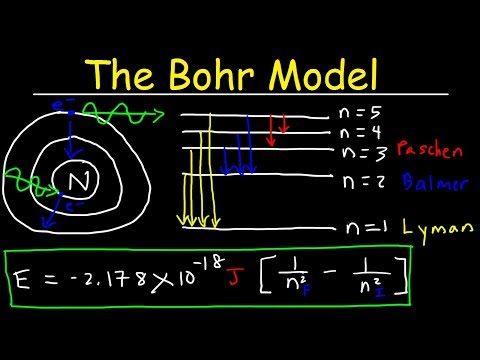
Bohr Model of the Hydrogen Atom
The Hydrogen Atom, Part 1 of 3: Intro to Quantum Physics
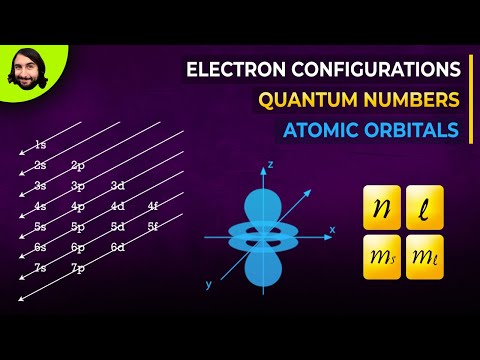
Quantum Numbers, Atomic Orbitals, and Electron Configurations
Quantum Chemistry 7.7 - Hydrogen Atom Radius
Quantum Chemistry 7
Quantum Chemistry 7.13 - Hydrogen Atom Term Symbols
Calculate the wavelength of the photon emitted when the hydrogen atom transition from n=5 to n=3.
Quantum Chemistry 7.6 - Hydrogen Atom Eigenvalues
Quantum Chemistry 7.2 - Hydrogen Atom Energies (Old Version)
Orbitals, Atomic Energy Levels, & Sublevels Explained - Basic Introduction to Quantum Numbers
Quantum Chemistry 7.0 - Hydrogen Atom Review (Old Version)
GENERAL CHEMISTRY explained in 19 Minutes
Quantum Chemistry 10.1 - Hydrogen Molecule Hamiltonian
The quantum mechanical treatment of the hydrogen atom gives the energy value:En =-13.6ev atom-1
Hydrogen 3: Eigenenergies
Lesson 3C 3 Hydrogen Atom Eigenvalues
How small are atoms?
Hydrogen full wavefunction (Phys 2D 2023-3-7)
A Better Way To Picture Atoms
Hydrogen R(r) (Phys 2D 2023-3-7)
Isaac Newton's INSANE Sleep Habits 😬
Quantum Chemistry 7.2 - Hydrogen Atom Energy Levels
Комментарии
 0:05:18
0:05:18
 0:21:44
0:21:44
 0:04:50
0:04:50
 0:18:35
0:18:35
 0:08:42
0:08:42
 0:12:39
0:12:39
 0:15:01
0:15:01
 0:04:17
0:04:17
 0:02:54
0:02:54
 0:07:25
0:07:25
 0:10:18
0:10:18
 0:11:19
0:11:19
 0:08:39
0:08:39
 0:18:49
0:18:49
 0:06:08
0:06:08
 0:05:48
0:05:48
 0:11:52
0:11:52
 0:10:44
0:10:44
 0:00:48
0:00:48
 0:28:14
0:28:14
 0:05:35
0:05:35
 0:28:25
0:28:25
 0:00:24
0:00:24
 0:06:19
0:06:19