To Understand the Fourier Transform, Start From Quantum Mechanics

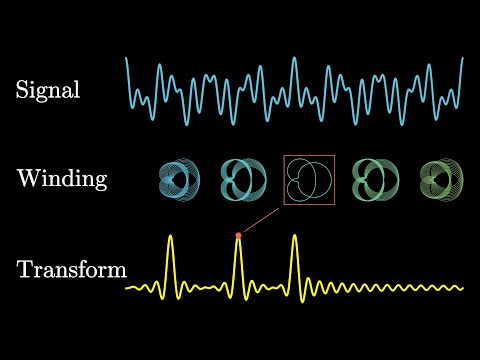
The Fourier transform has a million applications across all sorts of fields in science and math. But one of the very deepest arises in quantum mechanics, where it provides a map between two parallel descriptions of a quantum particle: one in terms of the position space wavefunction, and a dual description in terms of the momentum space wavefunction. Understanding this connection is also one of the best ways of learning what the Fourier transform really means.

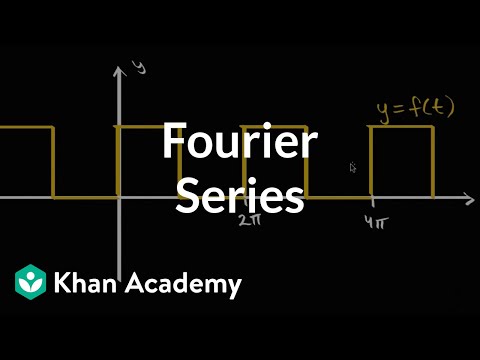
We'll start by thinking about the quantum mechanics of a particle on a circle, which requires that the wavefunction be periodic. That lets us expand it in a Fourier series---a superposition of many sine and cosine functions, or equivalently complex exponential functions. We'll see that these individual Fourier waves are the eigenfunctions of the quantum momentum operator, and the corresponding eigenvalues are the numbers we can get when we go to measure the momentum of the particle. The coefficients of the Fourier series tell us the probabilities of which value we'll get.

Then, by taking the limit where the radius of this circular space goes to infinity, we'll return to the quantum mechanics of a particle on an infinite line. And what we'll discover is that the full-fledged Fourier transform emerges directly from the Fourier series in this limit, and that gives us a powerful intuition for understanding what the Fourier transform means. We'll look at an example that shows that when the position space wavefunction is a narrow spike, so that we have a good idea of where the particle is in space, the momentum space wavefunction will be spread out across a huge range. By knowing the position of the particle precisely, we don't have a clue what the momentum will be, and vice-versa! This is the Heisenberg uncertainty principle in action.


0:00 Introduction
2:56 The Fourier series
16:08 The Fourier transform
25:37 An example

About me:

[Velthur-ct]

This has been extraordinary for me!!!! I am a 65-year-old nerd who studied chemical engineering and is now trying to understand quantum physics. This is almost as good as gaming!!!!

[MaxxTosh]

You seriously give 3B1B a run for his money, this is fantastic. I can’t wait to see more!

[ki-ka]

This is almost incomprehensibly beautiful on a number of levels.

[lewiswinner]

Amazing to get a deeper understanding of the Fourier transform, very thorough as always. THX!

[catamie]

😘💗😍💞😋😁😀😃😇😱😯😲✨🌟🎉💘💕Mathematical physics is my passion

[DudeWhoSaysDeez]

I have found the Fourier transform videos really interesting lately. I like that 3B1B, Veritasium, and you have all given a unique way to understand it.

[bobbyking]

I’m a second year chemistry graduate student and will be teaching quantum mechanics next semester. I will 100% be showing them this video alongside my own video “Demystifying Quantum Mechanics in 15 Minutes” Excellent stuff! I’m glad there are teachers like you in this world. Also, what program do you use to create to your animations. They’re’ beautiful. You’re both an artist and a scientist.

[alejrandom]

As a beginner in quantum mechanics, I love how this ties so many things. Extracting coefficients by taking an inner product with an eigenfunction, the kronecker delta, fourier... Really makes the fourier transform look like something very natural ♡

[johnchessant]

Amazing video! This is a great complement to 3blue1brown's videos on the Fourier transform where he looks at it from a math perspective.

[Paulakat]

I'm a negative zero of me learning this

[mintakan]

Outstanding use of visuals, along with how the transitions happen, when the quantities are varied.

[lewiswinner]

In our theoretical physics 2 class we actually started out with the Fourier transform and are now working our way towards the momentum space wave functions

[alejrandom]

So in some sense, a fourier transform is just a change of basis 🤔

[paulg]

For all of us teaching Fourier methods to engineers for circuits, signal processing and EM this is a fantastic way to bring in quantum mechanical examples as well.

[Jacked_R_Us]

I've been waiting long for a video like this thank you very much

[mario]

2:24 Please… never pronounce “i” as (-1)^0.5… i^2 = -1… it isn’t the same backwards.

[AbuSousPR]

As a telecommunication engineer... I was stunned when I 1st saw Schrodinger's wave equation. Stunned
The frequency transform is just another form of a probability function. Actually we use the term probability density function & power density function interchangeably

in Much of digital signal processing & communications theorems; that is all we care about to do filter designs🖐

your video highlights this and many other good ideas.

BTW.Heisenberg's's uncertainty principle..arises well in wavelet theory too

edited:

by the way... you have explained how when sine waves are integer multiple... they make orthogonal functions

believe it or not... this is the core idea behind 4G LTE technology ✌️

orthogonal is used to reduce noise generated by inter-symbol interference

[wdavis]

I took a class on Fourier Tranforms my junior year. Unfortunately our professor, while being a nice guy, was probably was the single worst teacher I've ever had. I left that class more confused and disinterested than anything else. I'm fortunate that videos like this exist. So many years later I've grown to comprehend and enjoy this part of math that initially confused and frustrated me. Thanks for the very informational upload!

[Guido_XL]

Very well explained! I already knew Fourier Transform from my background, which partly entails signal-processing, which also pointed me into the direction of Wavelet Transformation. But I must confess that my intuitive grasp was not yet firm enough as to pretend that I really understood it all. This video is one of those rare gems that support many interested non-academics and engineers out there that are looking for good explanations. Thank you so much!

[johnnyboy-fv]

Incredible description, incredible graphics, incredible explanation. Simply beautiful. So much work must have gone into this labour of love. Thank you.