filmov
tv
Partial fractions integral with long division and repeated linear factor in denominator.
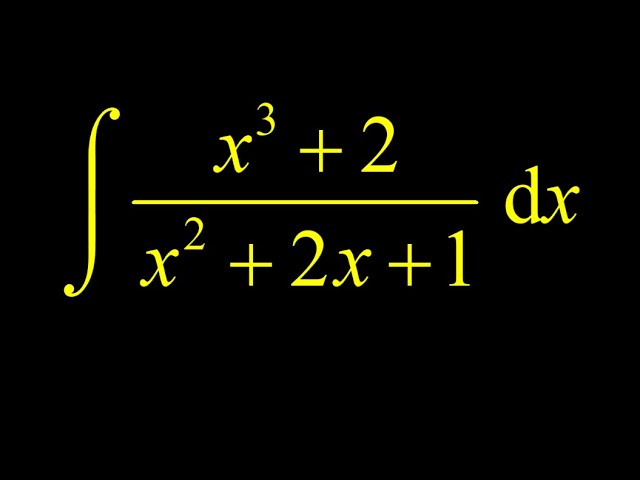
Показать описание
Computing the indefinite integral (x^3+2)/(x^2+2x+1): a partial fractions integral with long division and repeated linear factor.
When we compute the integral of a rational expression, the natural tool is partial fractions decomposition. However, we have to make sure the rational expression is "proper", meaning the degree of the numerator is less than the degree of the denominator.
In this partial fractions integral, the degree of the numerator is three and the degree of the denominator is 2, so we need to start by using long division to obtain a new rational expression that is proper.
We apply polynomial long division to the integral and obtain a linear term, a constant, and a proper rational expression. Now we can use partial fractions decomposition! We factor the denominator, and we end up with a repeated linear factor in denominator. We propose the partial fractions decomposition for repeated factors.
To solve for the constants in the partial fractions decomposition, we multiply by the least common denominator and compare coefficients of powers of x. We quickly obtain both undetermined constants in the partial fractions decomposition.
Finally, we rewrite the integral using the partial fractions decomposition, and we integrate each piece. Each term is quickly computed using the power rule or the natural log rule, and we're done!
When we compute the integral of a rational expression, the natural tool is partial fractions decomposition. However, we have to make sure the rational expression is "proper", meaning the degree of the numerator is less than the degree of the denominator.
In this partial fractions integral, the degree of the numerator is three and the degree of the denominator is 2, so we need to start by using long division to obtain a new rational expression that is proper.
We apply polynomial long division to the integral and obtain a linear term, a constant, and a proper rational expression. Now we can use partial fractions decomposition! We factor the denominator, and we end up with a repeated linear factor in denominator. We propose the partial fractions decomposition for repeated factors.
To solve for the constants in the partial fractions decomposition, we multiply by the least common denominator and compare coefficients of powers of x. We quickly obtain both undetermined constants in the partial fractions decomposition.
Finally, we rewrite the integral using the partial fractions decomposition, and we integrate each piece. Each term is quickly computed using the power rule or the natural log rule, and we're done!
 0:41:07
0:41:07
 2:55:43
2:55:43
 0:05:18
0:05:18
 0:19:09
0:19:09
 0:07:19
0:07:19
 0:09:08
0:09:08
 0:50:59
0:50:59
 0:50:06
0:50:06
 0:11:19
0:11:19
 0:09:51
0:09:51
 0:09:14
0:09:14
 0:04:44
0:04:44
 0:11:05
0:11:05
 0:06:08
0:06:08
 0:18:24
0:18:24
 0:28:40
0:28:40
 0:11:53
0:11:53
 1:00:01
1:00:01
 0:14:12
0:14:12
 0:18:07
0:18:07
 0:05:59
0:05:59
 0:32:24
0:32:24
 0:01:01
0:01:01
 0:44:09
0:44:09