filmov
tv
How to Solve Schrodinger's Equation for the Infinite Square Well Potential

Показать описание
Subscribe for more physics content!
We solve Schrodinger's Equation in the 1D infinite square well potential. This potential, defined from 0 to L, allows us to illustrate the concept of energy quantization. This is one of the few analytically solvable potentials in quantum mechanics and serves as an excellent introduction to the differences between classical systems and quantum systems.
To solve the potential, we assume an exponential solution to a second-order linear homogenous ordinary differential equation. After plugging in this ansatz, we can obtain the value of an exponentiated constant. Using the boundary conditions of the infinite well, as well as normalization (square integration) of the wavefunction, we obtain the remaining constants of our solution - and also explicitly see what energy quantization means! Lastly, we graph the stationary states n = 1 to n = 4, and discuss some of the implications of this solution!
Animations were made using the Python-based animation engine of 3Blue1Brown, Manim.
Songs:
Otis - Lambert
Sleeping Lotus - Joep Beving
Oasis - Wonderwall (Lambert Rework)
Tags:
#physics
#quantum
#quantumphysics
#quantummechanics
#schrodinger
#schrodingersequation
#schrodingerscat
#differential
#differentialequations
#linear
#homogenous
#mathematics
#math
#manim
#3blue1brown
#3b1b
#science
#mathanimations
#physicsanimations
#physicshomework
#physicsmajor
#undergrad
#collegephysics
#wave
#probability
#particle
#tunneling
#superposition
#electron
#eigenstates
#energy
#Heisenberg
#Bohrmodel
#deBroglie
#Planck's
#photons
#waveparticle
#light
#interference
#diffraction
#differential
#math
#solving
#solve
#schrodinger
#blakepi
#blakepiphysics
#animatedphysics
#mathematics
#science
#ansatz
#ode
#pde
#partial
#separation
#variables
#classical
We solve Schrodinger's Equation in the 1D infinite square well potential. This potential, defined from 0 to L, allows us to illustrate the concept of energy quantization. This is one of the few analytically solvable potentials in quantum mechanics and serves as an excellent introduction to the differences between classical systems and quantum systems.
To solve the potential, we assume an exponential solution to a second-order linear homogenous ordinary differential equation. After plugging in this ansatz, we can obtain the value of an exponentiated constant. Using the boundary conditions of the infinite well, as well as normalization (square integration) of the wavefunction, we obtain the remaining constants of our solution - and also explicitly see what energy quantization means! Lastly, we graph the stationary states n = 1 to n = 4, and discuss some of the implications of this solution!
Animations were made using the Python-based animation engine of 3Blue1Brown, Manim.
Songs:
Otis - Lambert
Sleeping Lotus - Joep Beving
Oasis - Wonderwall (Lambert Rework)
Tags:
#physics
#quantum
#quantumphysics
#quantummechanics
#schrodinger
#schrodingersequation
#schrodingerscat
#differential
#differentialequations
#linear
#homogenous
#mathematics
#math
#manim
#3blue1brown
#3b1b
#science
#mathanimations
#physicsanimations
#physicshomework
#physicsmajor
#undergrad
#collegephysics
#wave
#probability
#particle
#tunneling
#superposition
#electron
#eigenstates
#energy
#Heisenberg
#Bohrmodel
#deBroglie
#Planck's
#photons
#waveparticle
#light
#interference
#diffraction
#differential
#math
#solving
#solve
#schrodinger
#blakepi
#blakepiphysics
#animatedphysics
#mathematics
#science
#ansatz
#ode
#pde
#partial
#separation
#variables
#classical
Комментарии
 0:13:04
0:13:04
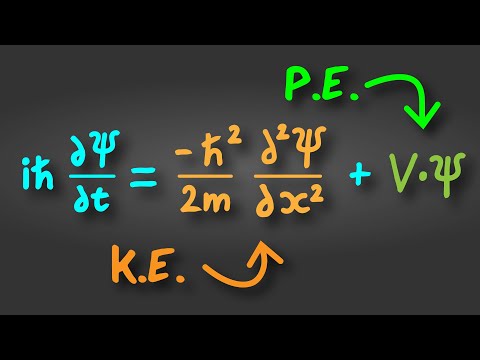 0:01:00
0:01:00
 0:06:28
0:06:28
 0:20:59
0:20:59
 0:14:13
0:14:13
 0:49:30
0:49:30
 0:00:59
0:00:59
 0:10:19
0:10:19
 0:15:48
0:15:48
 0:16:35
0:16:35
 1:27:34
1:27:34
 0:26:32
0:26:32
 0:04:38
0:04:38
 0:09:28
0:09:28
 0:29:55
0:29:55
 0:14:35
0:14:35
 0:10:11
0:10:11
 0:05:35
0:05:35
 0:55:36
0:55:36
 0:01:00
0:01:00
 0:17:27
0:17:27
 0:12:19
0:12:19
 0:10:46
0:10:46
 0:09:29
0:09:29