Vectors and the Geometry of Space: The Dot Product

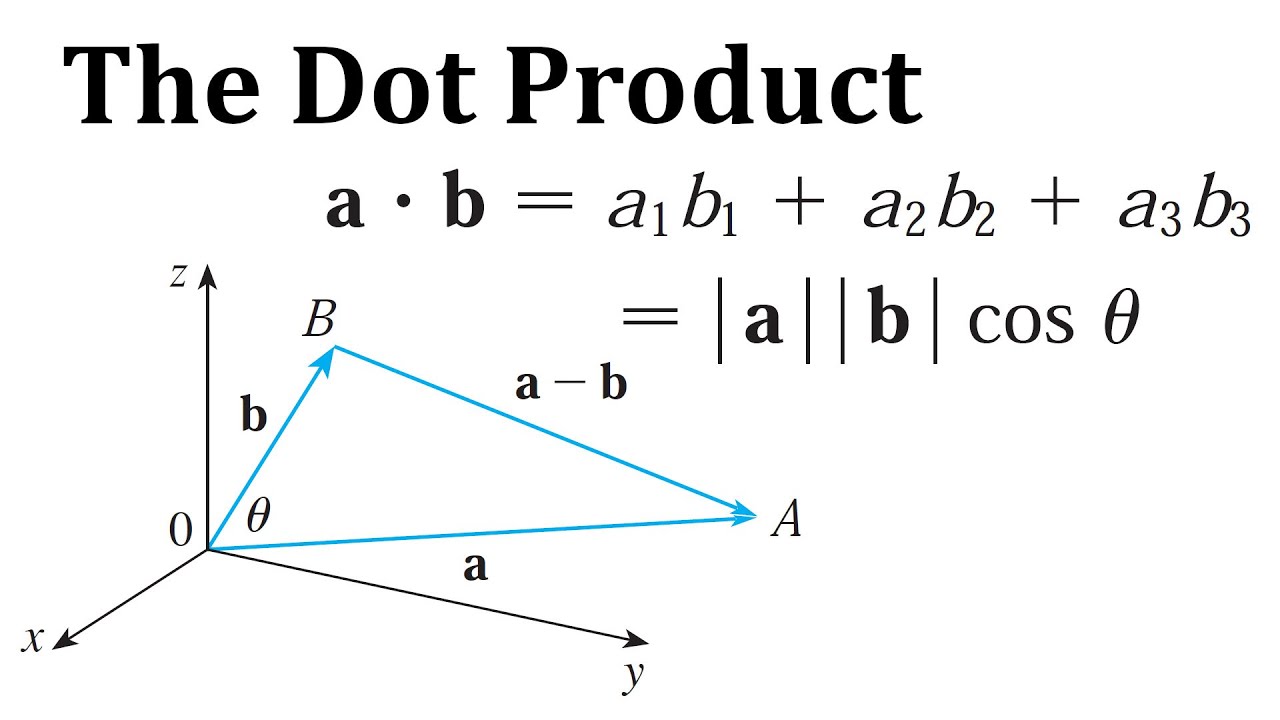
In this video I go over further into vectors and this time look at multiplying vectors with the dot product. In my previous videos I discussed adding vectors and multiplying vectors with a scalar. This time I discuss multiplication of two vectors via the dot product, which is defined as multiplying all corresponding vector components and adding them up, thus giving a scalar or real number value; aka not a vector. Further in the video I show that this way of defining vector multiplication has useful applications since it can be reinterpreted in terms of the angle between 2 vectors. I also discuss vector projections, direction cosines, and applications to physics of the dot product.

The topics covered as well as their timestamps are listed below.

- Introduction: 0:00
- Sections in Calculus Book Chapter: 1:03
- Topics to Cover: 1:46
1. The Dot Product: 2:52
- Definition 1: Dot Product: 3:38
- Example 1: 6:15
- Properties of the Dot Product: 10:49
- Proof of Property 1: 12:42
- Proof of Property 2: 14:00
- Proof of Property 3: 15:59
- Proof of Property 4: 19:15
- Proof of Property 5: 24:00
- Geometric Interpretation of the Dot Product: 24:45
- Definition 2: Dot Product: 28:02
- Example 2: 43:14
- Corollary: 45:46
- Example 3: 46:49
- Perpendicular Vectors: 52:42
- Example 4: 54:47
2. Vector Angles: 56:49
- Direction Angles and Direction Cosines: 1:02:55
- Example 5: 1:17:28
3. Projections: Vector and Scalar Projections: 1:21:27
- Summary of Projections: 1:30:22
- Example 6: 1:33:19
4. Vectors in Physics: 1:39:04
- Example 7: 1:42:33
- Example 8: 1:45:25

Related Videos:

------------------------------------------------------

[mes]

In this video I go over further into vectors and this time show how to multiply two vectors with the concept of the dot product.

[FengMarc]

a question about vector projections:
1. proj_a(b) = comp_a(b) · (a/|a|)
2. comp_a(b) = (a · b) / |a|
3. Because 1 and 2 are true, proj_a(b) = ((a · b) / |a|) · (a/|a|)
4. Because 3 is true, proj_a(b) = ((a · a · b)) / (|a| · |a|)
5. Property of dot products state that a · a = |a|^2
6. |a| · |a| = |a|^2
7. Because 4, 5, 6 are true, proj_a(b) = (|a|^2 · b) / (|a|^2)
8. Simplify the equation from 7, I got proj_a(b) = b, which is apparently wrong... which step went wrong here?