filmov
tv
The most useful polynomials you have never heard of.
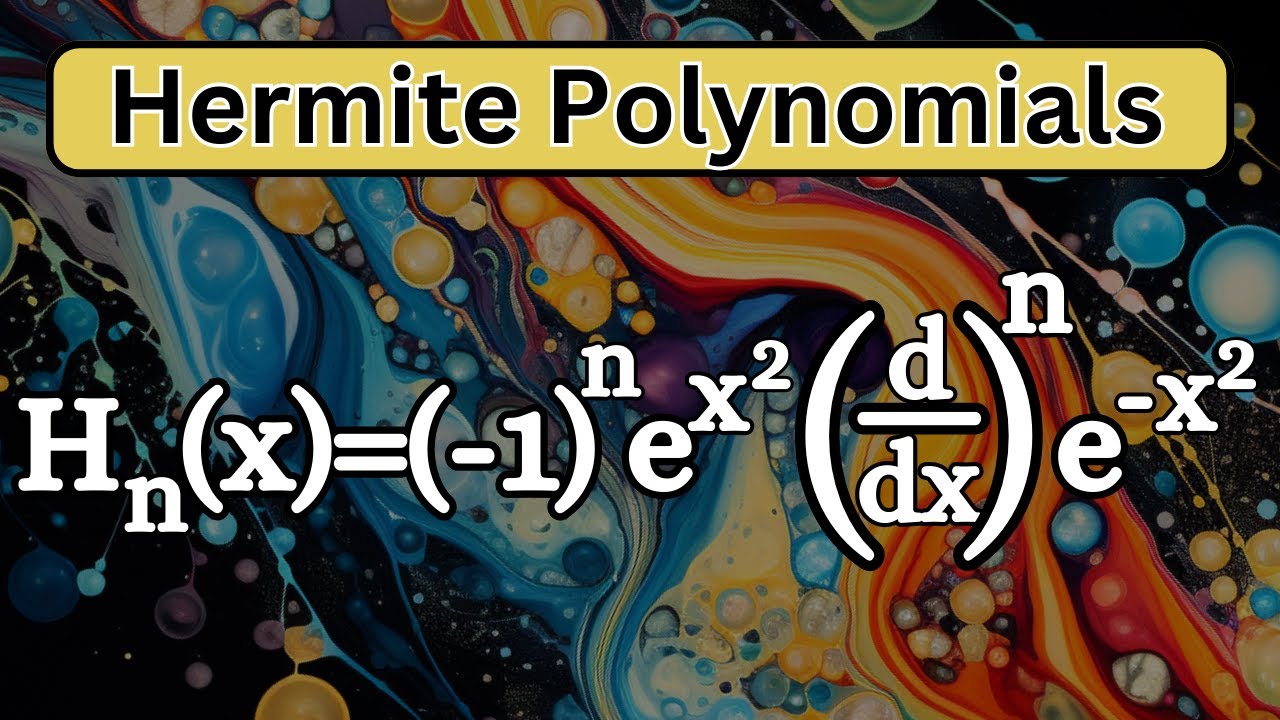
Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
The most useful polynomials you have never heard of.
What are POLYNOMIALS used for? REAL LIFE Situations | Animated Introduction to Polynomials (Part 1)
Algebra Basics: What Are Polynomials? - Math Antics
What is important to know about polynomials?
AP Scores are out today
you haven't seen this before! @blackpenredpen
Can you factor this polynomial? One of the most important things you need to know in Algebra!
Grant Sanderson (3Blue1Brown): Best Way to Learn Math | AI Podcast Clips
Polynomials in 20 Minutes! | Class 10 Board Exam Preparation | One Shot Lecture 🎯
Intro to Polynomials (Binomial, Trinomial), Degrees & Simplifying - Fast Method
The Most Important Math Formula For Understanding Physics
Polynomials (1 of 3: Introduction to Polynomials)
How to solve a polynomial inequality?
Reproduction Ka practical 😅😂 Funniest moments during Online class #alakhpandey #physicswallah
Undirected graphs can't equal a polynomial... or can they?
FACTOR POLYNOMIALS (Funny Animated Story 😂) - Learn in 8 min!
Do You Know This About Polynomial??🧐🧐 #Shorts #PhysicsWallah
1st Fundamental Theorem of Calculus | AP Calculus | Calculus 1 #shorts
Understand Calculus in 1 minute
Polynomials – The BIG PICTURE…you need know….
Find f(2) of the function using the Remainder Theorem! Algebra Polynomial Theory!
Polynomials (2 of 3: Adding & Subtracting Polynomials)
Let’s Factor the Polynomial Step by Step
All You Need to Know About Multiplying Polynomials by Shmoop
Комментарии
 0:20:26
0:20:26
 0:05:25
0:05:25
 0:11:09
0:11:09
 0:16:44
0:16:44
 0:00:51
0:00:51
 0:00:53
0:00:53
 0:14:49
0:14:49
 0:03:22
0:03:22
 0:20:26
0:20:26
 0:26:44
0:26:44
 0:31:42
0:31:42
 0:09:38
0:09:38
 0:00:58
0:00:58
 0:00:16
0:00:16
 0:00:59
0:00:59
 0:08:51
0:08:51
 0:00:39
0:00:39
 0:01:01
0:01:01
 0:00:57
0:00:57
 0:22:50
0:22:50
 0:15:48
0:15:48
 0:07:19
0:07:19
 0:11:18
0:11:18
 0:03:54
0:03:54