filmov
tv
6. Linear Algebra: Vector Spaces and Operators (continued)

Показать описание
MIT 8.05 Quantum Physics II, Fall 2013
Instructor: Barton Zwiebach
In this lecture, the professor talked about linear operators and matrices, etc.
License: Creative Commons BY-NC-SA
Instructor: Barton Zwiebach
In this lecture, the professor talked about linear operators and matrices, etc.
License: Creative Commons BY-NC-SA
Understanding Vector Spaces
6. Linear Algebra: Vector Spaces and Operators (continued)
Vector Spaces Explained | Linear Algebra
Abstract vector spaces | Chapter 16, Essence of linear algebra
Linear combinations, span, and basis vectors | Chapter 2, Essence of linear algebra
Linear subspaces | Vectors and spaces | Linear Algebra | Khan Academy
Linear Transformations on Vector Spaces
Vectors | Chapter 1, Essence of linear algebra
Elementary Linear Algebra Lecture 16 - Euclidean Vector Spaces (part 1)
4.1 Vector Spaces and Subspaces
Linear combinations and span | Vectors and spaces | Linear Algebra | Khan Academy
Linear Algebra Column Space
Finding the Dimensions of a Matrix 📚 #Shorts #linearalgebra #math #maths #mathematics #education
Vector Spaces | Definition & Examples
5. Linear Algebra: Vector Spaces and Operators
What is a vector space? -- Abstract Linear Algebra 6
Eigenvectors and eigenvalues | Chapter 14, Essence of linear algebra
Linear Algebra 6.1.1 Inner Product, Vector Length and Distance
Elementary Linear Algebra Lecture 21 - Euclidean Vector Spaces (part 6)
What is a vector?
Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra
Oxford Linear Algebra: Direct Sum of Vector Spaces
1.2 Vector Spaces - #06 N-Dimensional Vector Spaces (Special)
Lecture 6: Linear Algebra ( Linear combinations of vector. )
Комментарии
 0:08:41
0:08:41
 1:20:34
1:20:34
 0:17:30
0:17:30
 0:16:46
0:16:46
 0:09:59
0:09:59
 0:23:29
0:23:29
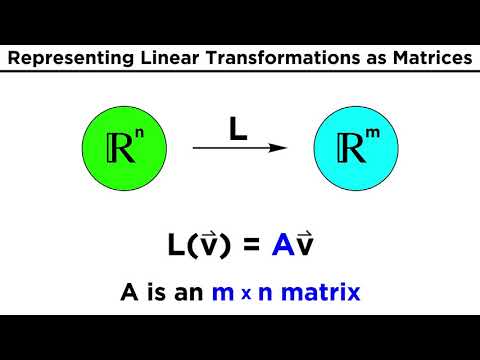 0:09:11
0:09:11
 0:09:52
0:09:52
 0:23:23
0:23:23
 1:14:57
1:14:57
 0:20:35
0:20:35
 0:00:56
0:00:56
 0:00:12
0:00:12
 0:08:11
0:08:11
 1:22:12
1:22:12
 0:47:53
0:47:53
 0:17:16
0:17:16
 0:12:25
0:12:25
 0:15:43
0:15:43
 0:00:26
0:00:26
 0:12:09
0:12:09
 0:30:52
0:30:52
 0:18:57
0:18:57
 0:03:42
0:03:42