filmov
tv
A Nice Math Olympiad System of Equations - Simplified!
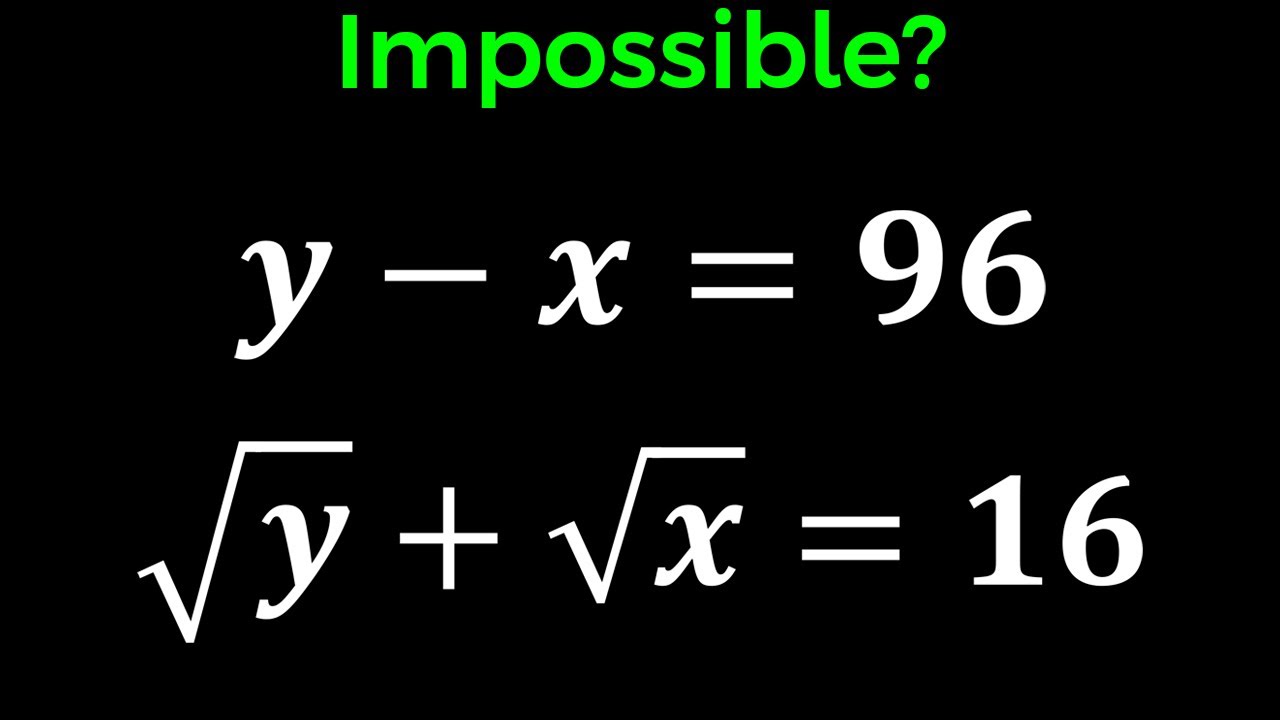
Показать описание
In this math algebra video, we will solve a mathematics Olympiad system of equations.
A Nice Math Olympiad Question | Quick!!!
A Nice Math Olympiad Problem | What Is The Value Of 'a' and 'b' In This Problem?...
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
A Nice Math Problem With Exponents| Math Olympiad
A Nice Diophantine System | Math Olympiads
A Nice Exponential System | Math Olympiads
Français | Math Olympiad | A Nice Algebra Problem
A Nice and Simple Equation in National Maths Olympiad
Nice Exponential Simplification Math Problem | No Calculator | Olympiad Mathematics
A Nice Math Olympiad Algebraic Expansions Problem. #math #olympiad #mathematics #matholympiad #viral
System of Exponential Equations | A Nice Algebra Challenge | Math Olympiad Exam
Math Problem Test your IQ 🧠 #olympiad #maths #jee #iitjee
Luxembourg - Math Olympiad Question | You should know this trick
Norway Math Olympiad Question | You should be able to solve this!
A Nice and Symmetric Equation | Polish Mathematical Olympiad Second Round
A Nice Mathematics algebra problem | Olympiad Question | rational problem | x=?
Math Olympiad Problem | A Nice Algebra Challenge
A Nice Math Olympiad Algebra Problem | You should learn this trick?
A Nice Math Olympiad Problem | What Is The Value Of 'a' and 'b' In This Problem?...
Olympiad Mathematics - A Nice Algebra Problem | Sweden Junior Math Olympiad
A Nice Exponential Problem • Evaluate #shorts #olympiad #math #mathtrick #mathproblem #mathematics
Math Olympiad 3^m–2^m=65 | Math Olympiad Problems | Algebra
A Nice Easy Exponential Simplification Math Problem. #shorts #maths #exponential #olympiad #viral
Math Olympiad Question | Nice Algebra Equation | You should know this trick!!
Комментарии
 0:09:27
0:09:27
 0:12:40
0:12:40
 0:00:52
0:00:52
 0:03:12
0:03:12
 0:08:37
0:08:37
 0:09:32
0:09:32
 0:11:59
0:11:59
 0:07:41
0:07:41
 0:05:07
0:05:07
 0:00:51
0:00:51
 0:10:12
0:10:12
 0:00:32
0:00:32
 0:02:51
0:02:51
 0:03:21
0:03:21
 0:07:35
0:07:35
 0:14:39
0:14:39
 0:09:51
0:09:51
 0:09:31
0:09:31
 0:09:33
0:09:33
 0:02:37
0:02:37
 0:00:46
0:00:46
 0:10:49
0:10:49
 0:00:50
0:00:50
 0:07:26
0:07:26