filmov
tv
Derivative of log X = 1 / X Proof in Calculus

Показать описание
Derivative of log x to the base e is equal to 1/x. To find the derivative of log x we use first principle method of derivative calculus math.Derivative of log x is very important in derivative calculus.
Derivative of log x with any Base Explained | Calculus 1
Derivative of Logarithmic Functions
Take the derivative of the natural log function
Derivatives of Logarithmic and Exponential Functions
Proof of the Formula for the Derivative of Log Base a of x
differentiation of log x | differentiation of logarithmic functions | derivative of log x
Proof: Derivative of log(x)
How to find the derivative of logx
L17 KCET 2025 Maths Course | Continuity & Differentiability- 4 | Differentiation, ITF, Exponenti...
Derivative of log with arbitrary base
Differentiating Logarithmic Functions
How to differentiate y equals log x (log base 10)
Introduction to Logarithmic Differentiation
Find the second order derivative of the function log (log x) Ncert continuity and Differentiation
The Derivative of the Logarithm Base a of x
Find second derivative of log x Calculus
Derivative of log x from First Principle | Class 11 Maths | JP Sir
Derivative of log x #Shorts
Derivative of log(x) by method of first principle
Derivative Of logx with base 'a'| Differentiation Of log x with base a | Differentiation C...
Derivative of ln(1/x), calculus 1 tutorial
Proof of the derivative of log x
derivative of log base 10 of (x^3+1), with the box
how do we know the derivative of ln(x) is 1/x (the definition & implicit differentiation)
Комментарии
 0:04:43
0:04:43
 0:12:13
0:12:13
 0:00:43
0:00:43
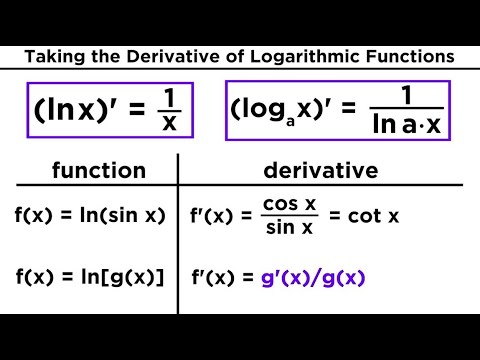 0:08:41
0:08:41
 0:02:45
0:02:45
 0:00:30
0:00:30
 0:02:44
0:02:44
 0:02:22
0:02:22
 1:44:34
1:44:34
 0:02:47
0:02:47
 0:05:00
0:05:00
 0:00:49
0:00:49
 0:13:31
0:13:31
 0:02:15
0:02:15
 0:01:53
0:01:53
 0:02:35
0:02:35
 0:05:14
0:05:14
 0:00:41
0:00:41
 0:02:29
0:02:29
 0:04:28
0:04:28
 0:00:52
0:00:52
 0:04:28
0:04:28
 0:02:15
0:02:15
 0:16:49
0:16:49