filmov
tv
Integral of e^-x ln(x) from 0 to infinity

Показать описание
In this video, I evaluate the integral from 0 to infinity of e^(-x) ln(x) dx using power series. The answer is quite surprising and unexpected, so check it out! Enjoy!
Note: This video is used in the evaluation of the Vardi integral, which I'll do in a later video
Note: This video is used in the evaluation of the Vardi integral, which I'll do in a later video
Integral of e^-x ln(x) from 0 to infinity
can we do the integral of e^x*ln(x)? Hint: use integration by parts & a special function
integral e^x*lnx. Integral no elemental.
Integral of e^x/x vs. integral of 1/ln(x)
Integral of lnx
integral of e^e^x vs integral of ln(ln(x))
Integral of ln(x) fast!
Integral of ln(x) with a twist! #integrals #mathchallenge #mathtricks #calculus #calculushelp
Calculus 1 Exam Review Part5'
Ex: Definite Integral Using Integration by Parts in the Form x^n*ln(x)
Integrating Exponential Functions By Substitution - Antiderivatives - Calculus
PARTIELLE INTEGRATION ln(x) – integrieren, Logarithmus, Integral mit Grenzen lnx/x, x*lnx
Integral de (e^x)/x y ln(x)*e^x
Integral ln(x)
integral of e^x/(1+e^x)^2 vs. integral of ln(x)/(1+ln(x))^2 *hard*
Integration by Parts the Integral of xlnx
Integral of lnx/x
e^x und ln(x) Basics | Mathe by Daniel Jung
Defining the natural logarithm
Comparison test for improper integrals ex 3, integral of 1/ln(x) from e to inf, calculus 2 tutorial
Classic Integral ln(ln(x))/x #calculus #calculushelp #mathematics #integrationtricks #integrals
Minimum distance between e^x and ln(x)
ONE OF THE COOLEST INTEGRALS EVER!!! int ln(x)/(1+e^x) from 0 to infty
Integral of e^(ln(x)) | Integral of exp(ln(x)) | Integral of exponential of natural log of x
Комментарии
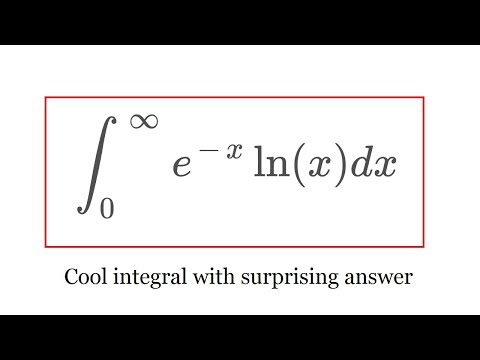 0:10:43
0:10:43
 0:04:50
0:04:50
 0:01:20
0:01:20
 0:08:48
0:08:48
 0:01:26
0:01:26
 0:03:59
0:03:59
 0:00:45
0:00:45
 0:00:56
0:00:56
 3:01:36
3:01:36
 0:06:18
0:06:18
 0:11:16
0:11:16
 0:10:26
0:10:26
 0:05:53
0:05:53
 0:00:24
0:00:24
 0:08:49
0:08:49
 0:02:07
0:02:07
 0:02:35
0:02:35
 0:05:11
0:05:11
 0:00:56
0:00:56
 0:11:07
0:11:07
 0:00:37
0:00:37
 0:03:14
0:03:14
 0:19:24
0:19:24
 0:01:41
0:01:41