filmov
tv
Linear Algebra 19r: Translations, or How to Represent Nonlinear Transformations by Matrix Products

Показать описание
Questions and comments below will be promptly addressed.
Linear Algebra is one of the most important subjects in mathematics. It is a subject with boundless practical and conceptual applications.
Linear Algebra is the fabric by which the worlds of geometry and algebra are united at the most profound level and through which these two mathematical worlds make each other far more powerful than they ever were individually.
Virtually all subsequent subjects, including applied mathematics, physics, and all forms of engineering, are deeply rooted in Linear Algebra and cannot be understood without a thorough understanding of Linear Algebra. Linear Algebra provides the framework and the language for expressing the most fundamental relationships in virtually all subjects.
This collection of videos is meant as a stand along self-contained course. There are no prerequisites. Our focus is on depth, understanding and applications. Our innovative approach emphasizes the geometric and algorithmic perspective and was designed to be fun and accessible for learners of all levels.
Numerous exercises will be provided via the Lemma system (under development)
We will cover the following topics:
Vectors
Linear combinations
Decomposition
Linear independence
Null space
Span
Linear systems
Gaussian elimination
Matrix multiplication and matrix algebra
The inverse of a matrix
Elementary matrices
LU decomposition
LDU decomposition
Linear transformations
Determinants
Cofactors
Eigenvalues
Eigenvectors
Eigenvalue decomposition (also known as the spectral decomposition)
Inner product (also known as the scalar product and dot product)
Self-adjoint matrices
Symmetric matrices
Positive definite matrices
Cholesky decomposition
Gram-Schmidt orthogonalization
QR decomposition
Elements of numerical linear algebra
I’m Pavel Grinfeld. I’m an applied mathematician. I study problems in differential geometry, particularly with moving surfaces.
Комментарии
 0:14:03
0:14:03
 0:03:42
0:03:42
 0:04:51
0:04:51
 0:11:32
0:11:32
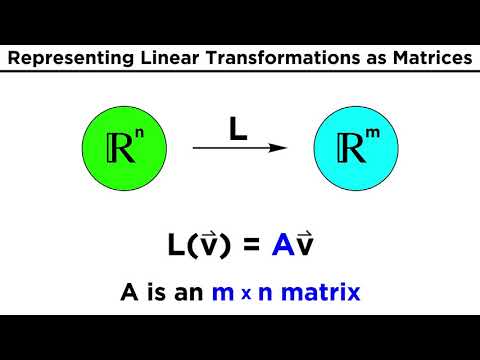 0:09:11
0:09:11
 0:09:23
0:09:23
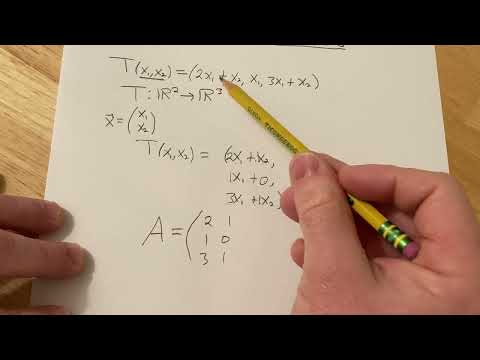 0:05:19
0:05:19
 0:00:28
0:00:28
 1:32:01
1:32:01
 0:47:28
0:47:28
 0:10:30
0:10:30
 0:12:40
0:12:40
 0:00:12
0:00:12
 0:05:58
0:05:58
 0:14:34
0:14:34
 0:13:37
0:13:37
 0:09:06
0:09:06
 0:07:39
0:07:39
 0:07:13
0:07:13
 0:05:47
0:05:47
 0:11:12
0:11:12
 0:10:19
0:10:19
 0:00:20
0:00:20
 0:00:48
0:00:48