filmov
tv
Linear Algebra 19m: Matrix Representation of a LT - Vectors in ℝⁿ, Eigenbasis

Показать описание
Linear Algebra 19m: Matrix Representation of a LT - Vectors in ℝⁿ, Eigenbasis
Linear Algebra 19g: Matrix Representation of a LT - the Algorithm Works!
Linear Algebra 19f: The Heart of Component Spaces - Matrix Representation of a Linear Tranformation
Linear Algebra 19k: Matrix Representation of a Linear Transformation - Vectors in ℝⁿ
Linear Algebra 19L: Matrix Representation of a LT - Vectors in ℝⁿ, Standard Basis
Linear Algebra 19i: Bad Basis! Bad Basis! Go to Your Room!
Linear Algebra 19t: I Once Was Blind, but Now Am Dilated
Complex Numbers As Matrices
Linear Algebra 19e: Illustration of Component Spaces by a Sum of Vectors in ℝⁿ
Linear Algebra 19p: Proof that Eigenbasis Yields a Diagonal Matrix
Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school
Linear Algebra 19c: Illustration of Component Spaces by a Sum of Geometric Vectors
Linear Algebra 19d: Illustration of Component Spaces by a Sum of Polynomials
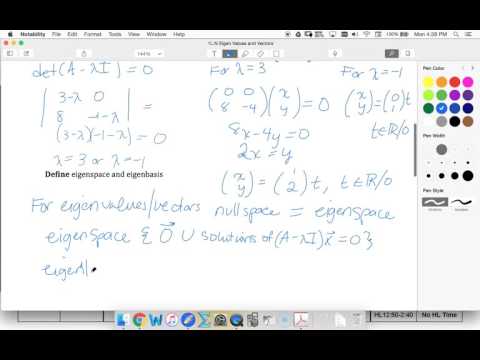
IB Further 1.9 Defining eigenspace and eigenbasis
Linear Algebra 19b: Component Spaces - Doing It Right!
Linear Algebra Showing that an eigenbasis makes for good coordinate systems
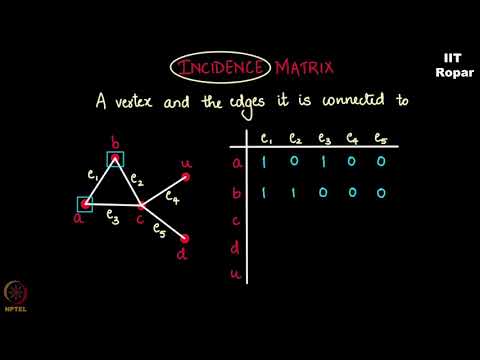
Incidence matrix representation mod08lec296
xavier memes #memes
Lecture 15b Eigenbases (finding an eigenbasis)
BEST DEFENCE ACADEMY IN DEHRADUN | NDA FOUNDATION COURSE AFTER 10TH | NDA COACHING #shorts #nda #ssb
Linear Algebra: Showing that an eigenbasis makes for good coordinate systems (Bangla)
Math 23a. Week 4, Video 2: Eigenbases & Matrix Diagonalization (4.4-4.5)
Tough times Never last 😊✌️ #delhipolice #motivation
Matrix Transformations and Determinants - Sections 2.4 and 2.5
Комментарии
 0:11:12
0:11:12
 0:06:22
0:06:22
 0:14:34
0:14:34
 0:12:40
0:12:40
 0:03:46
0:03:46
 0:08:36
0:08:36
 0:09:13
0:09:13
 0:09:21
0:09:21
 0:04:50
0:04:50
 0:07:28
0:07:28
 0:00:15
0:00:15
 0:16:41
0:16:41
 0:08:14
0:08:14
 0:03:16
0:03:16
 0:15:21
0:15:21
 0:13:09
0:13:09
 0:02:29
0:02:29
 0:00:06
0:00:06
 0:22:42
0:22:42
 0:00:15
0:00:15
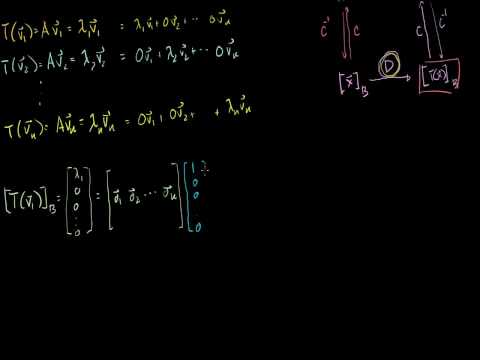 0:13:16
0:13:16
 0:12:06
0:12:06
 0:00:22
0:00:22
 0:08:19
0:08:19