filmov
tv
The Binomial Distribution: Mathematically Deriving the Mean and Variance

Показать описание
I derive the mean and variance of the binomial distribution. I do this in two ways. First, I assume that we know the mean and variance of the Bernoulli distribution, and that a binomial random variable is the sum of n independent Bernoulli random variables. I then take the more difficult approach, where we do not lie on this relationship and derive the mean and variance from scratch.
The Binomial Distribution: Mathematically Deriving the Mean and Variance
Binomial distribution | Probability and Statistics | Khan Academy
Binomial Distribution EXPLAINED with Examples
Binomial distributions | Probabilities of probabilities, part 1
Proof that the Binomial Distribution tends to the Poisson Distribution
Deriving the Binomial Distribution Probability Formula
Deriving the Binomial Distribution's Formula!
Binomial distribution: deriving the mean and standard deviation
An Introduction to the Binomial Distribution
Binomial Distribution Expected Value (Algebraic Derivation) | Probability Proofs
Binomial Distribution Mean and variance
Mean of the Binomial distribution using simple steps by easy maths easy tricks
The Poisson Distribution: Mathematically Deriving the Mean and Variance
An ingenious & unexpected proof of the Binomial Theorem (1 of 2: Prologue)
Binomial Distribution: Easy Proof of Mean and Variance | Engineering Mathematics
moment generating functions for binomial variables
The Normal Approximation to the Binomial Distribution
Introduction to the Negative Binomial Distribution
Proof of the mean of Binomial distribution
Binomial Distribution - Derivation of Mean, Variance & Moment Generating Function in English
Poisson distribution derivation. Intuitive example.
Probability | Proving Poisson Approximation to the binomial distribution | Conditions | Examples
Chapter 05: Introduction, derivation of the binomial distribution [2/4]
Introduction to Poisson Distribution - Probability & Statistics
Комментарии
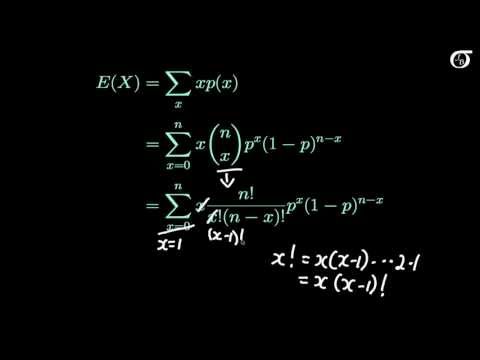 0:13:54
0:13:54
 0:11:51
0:11:51
 0:09:08
0:09:08
 0:12:34
0:12:34
 0:05:25
0:05:25
 0:15:51
0:15:51
 0:12:40
0:12:40
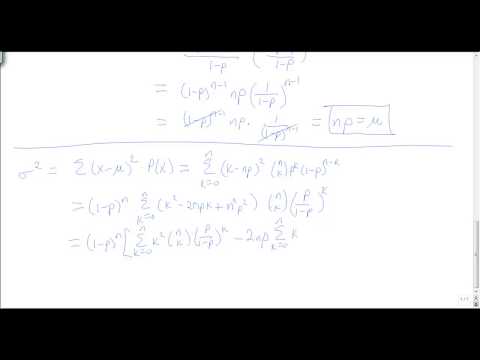 0:20:24
0:20:24
 0:14:11
0:14:11
 0:05:15
0:05:15
 0:13:21
0:13:21
 0:04:41
0:04:41
 0:09:17
0:09:17
 0:06:55
0:06:55
 0:19:04
0:19:04
 0:09:09
0:09:09
 0:14:10
0:14:10
 0:07:33
0:07:33
 0:06:40
0:06:40
 0:22:37
0:22:37
 0:08:52
0:08:52
 0:08:01
0:08:01
 0:10:01
0:10:01
 0:16:12
0:16:12