filmov
tv
Potential Functions, Fundamental Theorem of Calculus Applied to Line Integrals, & Path Independence

Показать описание
In this video we continue our discussion on line integrals by introducing the concept of potential functions which can be used to derive vector fields/functions. This allows us to apply the fundamental theorem of calculus to line integrals. We show that in this case, the line integral is independent of path (AKA the vector field is conservative).
Topics and timestamps:
0:00 – Introduction
0:35 – Potential functions
3:41 – Fundamental theorem of calculus applied to line integrals
13:15 – Example
29:49 – Conservative vector fields, relation to curl
#Calculus
Topics and timestamps:
0:00 – Introduction
0:35 – Potential functions
3:41 – Fundamental theorem of calculus applied to line integrals
13:15 – Example
29:49 – Conservative vector fields, relation to curl
#Calculus
Finding the scalar potential function for a conservative vector field // Vector Calculus
Conservative Vector Fields // Vector Calculus
Potential Functions, Fundamental Theorem of Calculus Applied to Line Integrals, & Path Independe...
The Fundamental Theorem of Line Integrals // Big Idea & Proof // Vector Calculus
Determining the Potential Function of a Conservative Vector Field
Finding a Potential for a Conservative Vector Field
How to Test if a Vector Field is Conservative // Vector Calculus
Multivariable Calculus: Fundamental Theorem of Line Integrals - Potential Functions (16.3)
Project Presentation | Tate Allen | Minimizing the standard Ring Axioms
How to use the fundamental theorem of line integrals when you have a conservative vector field.
Find Potential Function for Conservative Vector Field
potential function of the conservative vector field to evaluate a line integral (KristaKingMath)
Path Independence, Conservative VFs, Potential Functions, & Fundamental Theorem of Line Integral...
28 Conservative Fields, Potential Functions and The Fundamental Theorem of Line Integral
Path Independence, Conservative Fields, & Potential Functions
13.3 (8) The Fundamental Theorem of Line Integrals - Example #2: Finding the Potential (Part 1)
16.3: The FundamentalTheorem for Line Integrals
The Fundamental Theorem of Calculus
Real Analysis Lecture 61 Part 2: Existence of potential functions
potential function of a conservative vector field (KristaKingMath)
Fundamental Theorem for Line Integrals :: Conservative Vector Field Line Integral
30 Conservative Fields, Potential Functions and The Fundamental Theorem of Line Integral
Real Analysis Lecture 61 Part 1: The fundamental theorem of calculus for line integrals
Fundamental Theorem of Line Integrals
Комментарии
 0:12:06
0:12:06
 0:06:17
0:06:17
 0:36:06
0:36:06
 0:06:38
0:06:38
 0:06:57
0:06:57
 0:10:07
0:10:07
 0:05:30
0:05:30
 0:13:06
0:13:06
 0:46:16
0:46:16
 0:00:34
0:00:34
 0:03:55
0:03:55
 0:13:33
0:13:33
 0:17:38
0:17:38
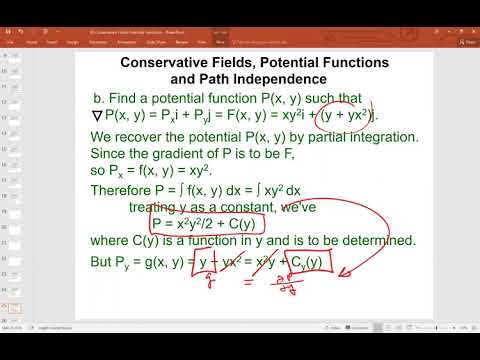 0:14:42
0:14:42
 0:45:46
0:45:46
 0:09:51
0:09:51
 0:43:34
0:43:34
 0:25:11
0:25:11
 0:31:36
0:31:36
 0:12:58
0:12:58
 0:08:09
0:08:09
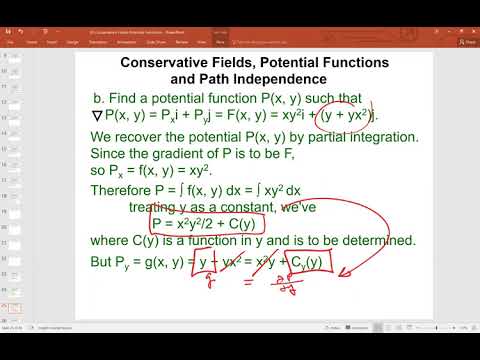 0:14:42
0:14:42
 0:17:24
0:17:24
 0:32:45
0:32:45