filmov
tv
Separation of Variables
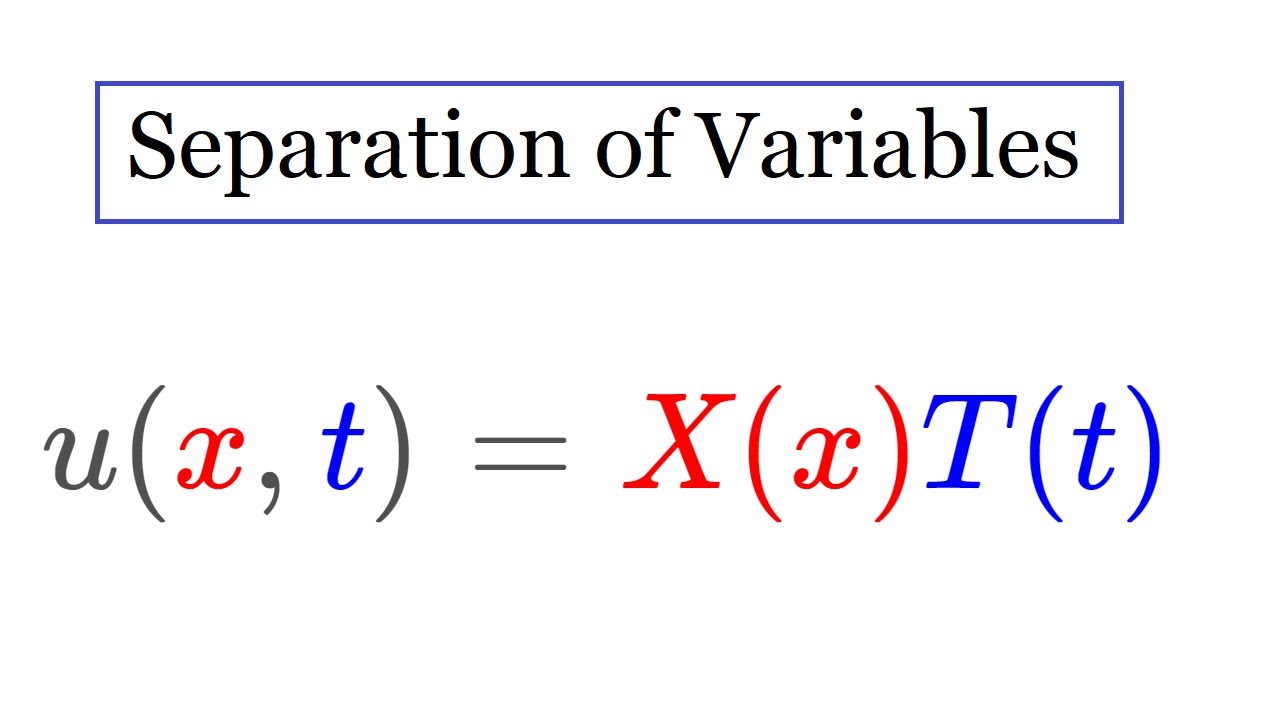
Показать описание
Separation of Variables for the Wave Equation
In this video, I illustrate the process of separation of variables by solving the wave equation on a finite interval with Neumann boundary conditions. Tune in for an adventure through PDEs, ODEs, and Fourier series! Enjoy
In this video, I illustrate the process of separation of variables by solving the wave equation on a finite interval with Neumann boundary conditions. Tune in for an adventure through PDEs, ODEs, and Fourier series! Enjoy
Separable First Order Differential Equations - Basic Introduction
Separation of Variables // Differential Equations
PDE 101: Separation of Variables! ...or how I learned to stop worrying and solve Laplace's equa...
Calculus AB/BC – 7.6 General Solutions Using Separation of Variables
PDE: Heat Equation - Separation of Variables
How To Solve Differential Equations | By Separation Of Variables
Oxford Calculus: Separable Solutions to PDEs
Separable Differential Equations (Differential Equations 12)
Solving an ODE using separation of variables
Differential Equations - Variable Separable DE Solved Problems
Separable differential equations introduction | First order differential equations | Khan Academy
Separation of Variables
Partial Differential Equations - II. Separation of Variables
Calculus 2 Lecture 8.1: Solving First Order Differential Equations By Separation of Variables
Differential Equations - Separation of Variables
Solved Problem #1 - Separation of Variables (Differential Equations)
Separation of variables
Solving the 1-D Heat/Diffusion PDE by Separation of Variables (Part 1/2)
PDE 13 | Wave equation: separation of variables
2.3 Separation of Variables
Separation of Variables
A-Level Maths: H7-02 Differential Equations: The Method of Separation of Variables
SEPARATION OF VARIABLES (VARIABLE SEPARABLE) | Differential Equations | TAGALOG-ENGLISH
Classical Electromagnetism | Lesson 2.3 | Separation of Variables - Cartesian
Комментарии
 0:10:42
0:10:42
 0:10:09
0:10:09
 0:49:54
0:49:54
 0:12:31
0:12:31
 0:21:17
0:21:17
 0:19:50
0:19:50
 0:21:25
0:21:25
 1:32:57
1:32:57
 0:06:29
0:06:29
 0:42:46
0:42:46
 0:09:05
0:09:05
 0:06:19
0:06:19
 0:09:24
0:09:24
 2:49:22
2:49:22
 0:07:16
0:07:16
 0:04:31
0:04:31
 0:11:28
0:11:28
 0:11:09
0:11:09
 0:19:08
0:19:08
 0:08:52
0:08:52
 0:48:34
0:48:34
 0:05:42
0:05:42
 0:23:26
0:23:26
 1:03:26
1:03:26