Geometric area bounded by two functions and a new way to use symmetry in an area integral.

Показать описание

00:00 Area between 1/sqrt(1-x^2) and (1+x): we compute the geometric area bounded by two functions and discover a new way to use symmetry in an area integral to obtain the same result produced by the standard area integral method. Note that "geometric area" means that we're counting area as inherently positive, rather than using signed area.

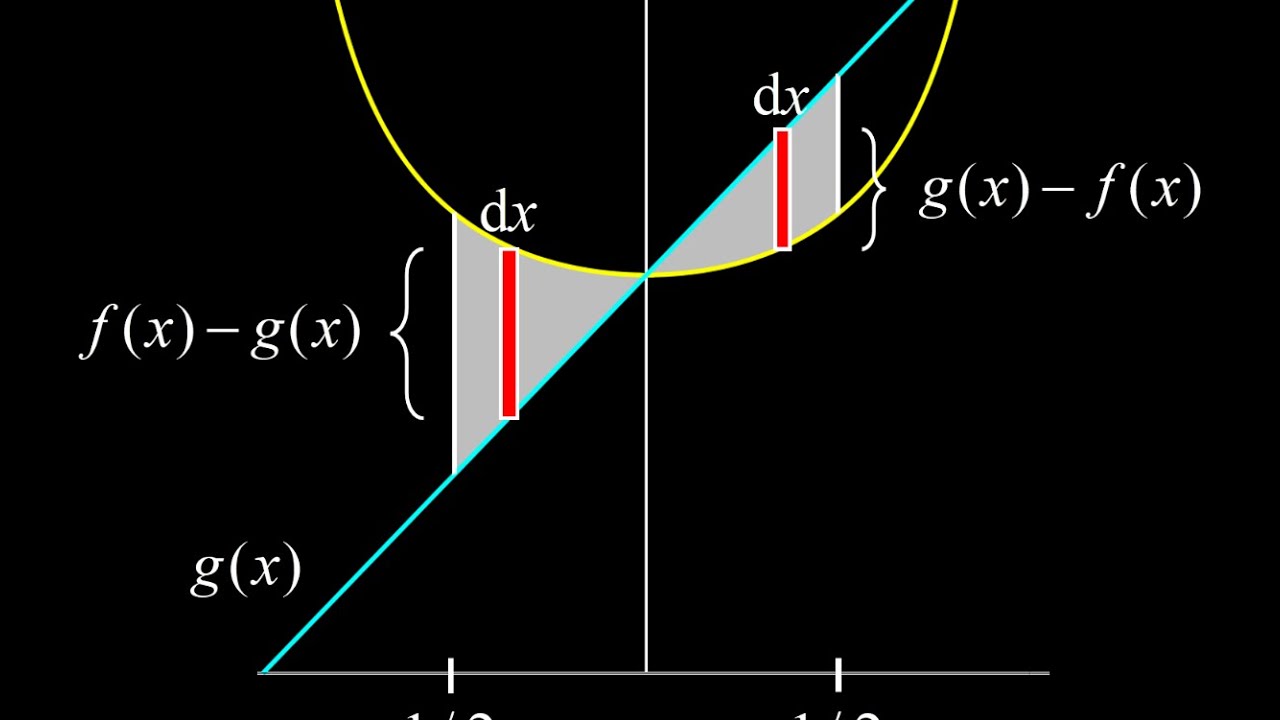
00:45 The standard approach to computing the area bounded by two functions: we split the integration interval at the intersection of the two functions, and we start with the left side of the area integral. We define a thin slice of the area dA as f(x)-g(x) to guarantee the area increment is positive, since f(x) is above g(x) on this interval. We set up the integral and guess the antiderivative, then apply the limits of integration to get the area. Note that the integral of 1/sqrt(1-x^2) gives us the inverse sine function.

04:43 A weird symmetry approach to the area between these functions: after noting that most of the terms cancel in the area integral, we start searching for an underlying symmetry in the problem to explain why so many things cancel. We find the symmetry by drawing a horizontal line through the intersection of the curves. This allows us to see that one part of the area on the left side can be transplanted to the right side to create a simple area under the function h(x)=x, and we compute this area, arriving at the same result with practically no work required.

06:07 Questions for the future: under what conditions does a symmetry approach like this actually apply? I'll think about it and make a video for that eventually.