Theorema Egregium: why all maps are wrong

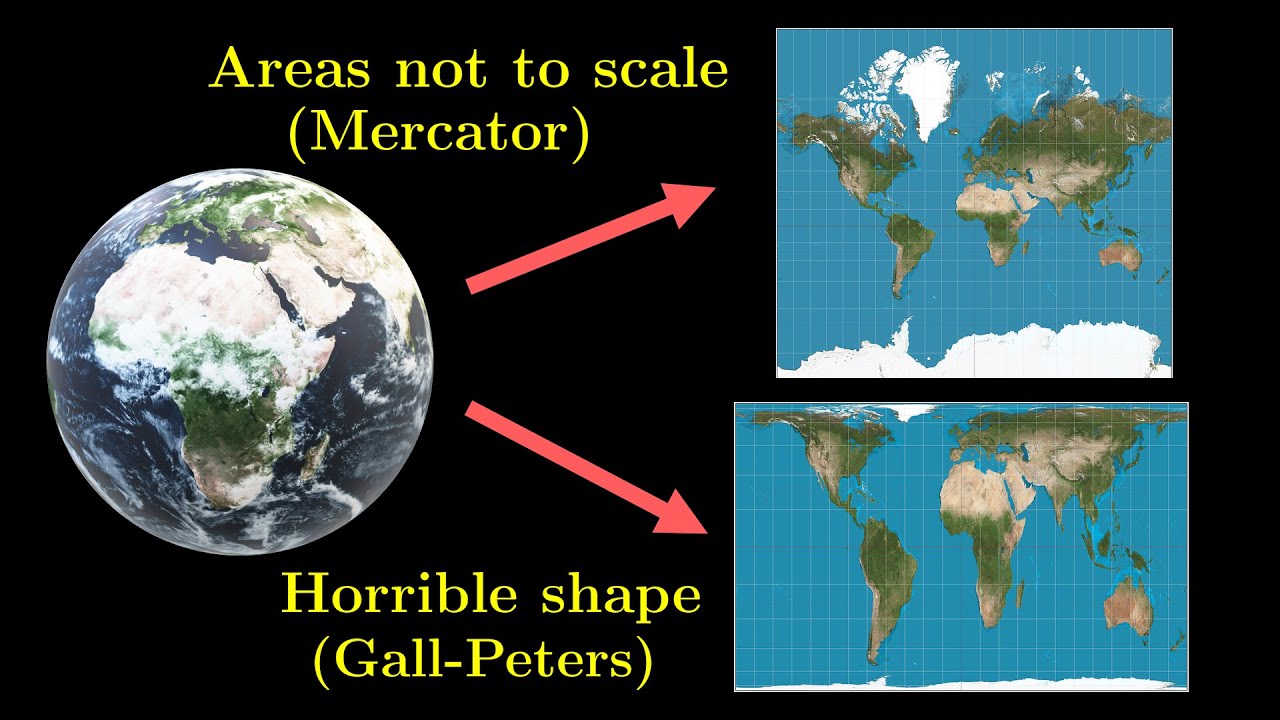
The Mercator projection is the standard world map, but it famously makes Greenland and Africa the same size, but in reality, Greenland is so much smaller. Gall-Peters projection aims to solve exactly this area mismatch problem, but the shape resulted is horrible, and actually unsuitable for any navigation, unlike Mercator. Can we make a world map that preserves both areas (like Gall-Peters) and angles (like Mercator)? No, and the reason why is Theorema Egregium, the subject of the video.

Traditionally, Theorema Egregium was proved with a lot of tedious calculations, and somehow magically, you can compute the curvature with the "first fundamental form", whatever that means. It took until more than a century later than its original discovery that a geometric proof was found, and is presented here.

Video chapters:
00:00 Introduction
02:40 Chapter 1: Curvature
10:32 Chapter 2: Spherical areas
17:34 Chapter 3.1: Gauss map preserves parallel transport
22:15 Chapter 3.2: Geodesics preserved
27:16 Chapter 3.3: Parallel transport preserved
31:46 Chapter 3.4: Area = holonomy on sphere
36:43 Chapter 4: Tying everything together
Other than commenting on the video, you are very welcome to fill in a Google form linked below, which helps me make better videos by catering for your math levels:

If you want to know more interesting Mathematics, stay tuned for the next video!

SUBSCRIBE and see you in the next video!

If you are wondering how I made all these videos, even though it is stylistically similar to 3Blue1Brown, I don't use his animation engine Manim, but I use PowerPoint, GeoGebra, and (sometimes) Mathematica to produce the videos.

Social media:

For my contact email, check my About page on a PC.

See you next time!

[mathemaniac]

Really did not want to make a 40-minute video, but also don't know how to split it up into two or more videos, so here we are. Theorema Egregium is my all-time favourite theorem, and it was traditionally proved using Christ-awful (a parody of the actual name Christoffel, because these symbols are tedious to calculate) symbols. So when I know of this geometric proof in Needham's book, I have to animate it.

[johnchessant]

Very satisfying proof, and I think a lot of it can be credited to how well-organized your presentation is! Also I wasn’t aware Needham wrote a second book!! This is excellent news (well I guess I’m 2 years late) and I can’t wait to get a copy

[benhsu]

Thanks you! I am starting down a differential geometry rabbit hole and the Theorema Egregium is one of the things motivating me to study this field. I'm sure I will find this video very useful in the year to come

[yonatanbeer]

Another great video! You've really been pumping out top notch videos recently, thank you!

[MCredstoningnstuff]

This was such an elegant and intuitive way to lay out the argument, thank you!

[dbp_patel_]

I read in one of your posts that you probably won't make videos on this and similar topics since they aren't performing well (i.e. fewer views). I am sure I am saying this on behalf of many other people here that please DO NOT STOP making these incredible videos. These videos mean a lot to people like me. And this kind of content deserves to be shared on a platform like YouTube with as many people as possible.

All the best for your PhD journey and I look forward to more videos on this and similar topics in the future.

Thank you for sharing and spreading the joy of learning maths.

[mathyland]

Great video! Early on I could tell this was inspired by Needham’s book. This is a good way to understand this proof without going through most of that book to get there.

[raulyazbeck]

One of my favorite theorems! Thanks for the video and the wonderful proof

[tetraedri_]

That was breathtakingly beautiful, thanks for sharing this proof!

[diribigal]

Never expected I'd be able to follow ideas behind this important theorem for maps and eating of pizza. Thanks for spreading awareness, and for animating and presenting this lovely proof.

[blacklistnr]

This video is really nicely animated! I also appreciate keeping the definitions+visualisations on screen like at 7:02 instead of jumping to a limit slide

[Yishay.S]

I usually don't comment but this video should be pushed forward.

Thank you for the efforts to make this more known.

It is a bit heavy for general youtube unfortunately.

I needed some time to listen through even though I am a math/physics major. ..

Hopefully I come back to this to follow thoroughly.

Thank you for put this out.

[blacklistnr]

@Intro's [no such map exists because it must preserve curvature]. That may be true mathematically, but not practically.

If you search something like "airplane routes", there are traffic hot spots(places where people want to have a map) and cold spots("lol, I didn't even notice that country was missing") so you could use those places to cut some seams to relax the necessary curvature, like in UV mapping, until the area/angle errors are less than x%.

After this whole process you can get an accurate flat map of the whole Earth*.

(*With some complaints from Pacific and Atlantic fish, but Greenland should have the right shape and size)

[mistertheguy]

This was great, I finally feel like I understand the course I took about this last semester!

[Anonymous-dfit]

a) Why is the curvature unitless? Shouldn't it be in inverse-square length units?
b) If two shapes have the same curvature everywhere, are they necessarily the same? Because I can imagine that maybe the area on the Gauss map is stretched in one direction and compressed in another, cancelling each other out, resulting in the same curvature despite being different shapes
c) Once you've proven that straight lines (minimal-length property) are preserved on a hypothetical area- and angle-preserving map, the rest of the proof is redundant. Any triangle on a sphere has a total angle greater than pi (indeed, the difference is the area in units of [earth's radius]^2). On a flat map, if you construct a triangle with straight lines and the three relevant areas, there must be a discontinuity somewhere. However, if you assume that the continuous points form contiguous sections of the map with a non-zero area, then you can put a triangle in that space, and repeat the argument, showing that one of the points aren't continuous, contradicting the premise. This means that given any area of the map, there must be a discontinuity somewhere; that is, they're dense on the map, which makes it completely useless

[moirai]

I've known about this theorem but resources like Wikipedia are so dry. Your video was excellent at explaining the Theorema Egregium!

[yds]

Interesting topic! Last video I watched about this was from the guy who's building Earth in Minecraft (he and the other builders spent a lot of time picking the best projection for the job, since Minecraft map is flat).

[petersmythe]

The Gall-Peters protection: because nothing says "not Eurocentric" like having the only regions with an accurate shape be at Latitude +- 45°

[Heuristicpohangtomars]

31:52 Gauss map preserves parallel transport Geodesics are preservedif areas and angles are Prallel transport preserved if areas and angles are. Holonomy of loop on sphere=area enclosed

[yinq]

What a wonderful video!
This theorem well deserves the name. And 2-d creatures actually can figure out if the world they're living on is flat or not. :P