filmov
tv
Suppose `a,b,c` are in AP and `a^(2),b^(2),c^(2)` are in GP, If `agtbgtc` and `a+b+c=(3)/(2)`,

Показать описание
Suppose `a,b,c` are in AP and `a^(2),b^(2),c^(2)` are in GP, If `agtbgtc` and `a+b+c=(3)/(2)`, than find the values of a and c.
Suppose \( a, b, c \) are in A.P. and \( a^{2}, b^{2}, c^{2} \) are in G.P. If \( abc \) and \( ...
Suppose a,b,c are in A.P and `a^2,b^2,c^2` are in G.P If `a ltb ltc` and `a+b+c=3/2` then the v...
Suppose a,b, c are in A.P. and a^(2) , b^(2),c^(2) are in G.P. if a lt b lt c and a+b+c =3/2, th...
Suppose `a,b,c` are in AP and `a^(2),b^(2),c^(2)` are in GP, If `agtbgtc` and `a+b+c=(3)/(2)`,
Progressions: If A, B and C are in A.P and b-a, c-b and an are in G.P then find a:b:c.
If the Numbers a, 7, b, 23, c are in AP. Find a, b and c
Suppose \( a, b, c \) are in A.P. and \( a^{2}, b^{2}, c^{2} \) are...
Let a,b,c be in AP and a^2,b^2,c^2 be in GP. If abc and a+b+c=3/2, then the value of a is
Suppose \( a, b, c \) are in A.P. and \( \mathrm{a}^{2}, \mathrm{~b}^{2}, \mathrm{c}^{2} \) are ...
Suppose \( a, b, c \) are in A.P. Let \( A, G \) be the arithmetic mean and geometric mean betwe...
If a,b,c are in A.P., b,c,d are in G.P. and 1/c , 1/d , 1/e are in A.P., prove that a,c,e are in G.P
If a, b, c are in AP and a^2, b^2, c^2 are in HP, then which of the following could hold true? (a...
If `(b+c)/a,(c+a)/b,(a+b)/c` are in `A.P.` show that `1/a,1/b1/c` are also in `A.P. (a +b+
Suppose the angles of a triangle \( A B C \) are in A.P. and sides \( b \) and \( c \) satisfy \...
Suppose the quadratic polynomial \( P(x)=a x^{2}+b x+c \) has positive coefficients \( a, b, c \...
JEE Main 2018 Maths Question - If a, b, c are in A.P. and a^{2},b^{2},c^{2} are in G.P. such that a
If a,b,c are in AP, show that ` (a(b+c))/(bc) , (b (c+a))/(ca), (c(a+b))/(ab)`, are also in AP.
If `a, b, c` are in A.P, then show that: `\ b c-a^2,\ c a-b^2,\ a b-c^2` are in A.P.
Suppose \( a, b \) and \( c \) are in A.P.. Let \( A \) and \( G \) be the arithmetic mean and g...
If `A,B,C` are in A.P then `(sinA-sinC)/(cosC-cosA)=`
If `a ,b ,c` are in A.P., then prove that the following are also in A.P. `a(1/b+1/c),b(1/c+1/a),c(1/
Lalit sir-jee a-circles-suppose ax+by+c=0 where a,b,c are in AP be normal to a family of circles
Suppose a=b^nc^m where a has dimensions lt
a,b,c are in AP and x, y, z are in G.P. the points (a,x), (b,y), (c,z) are collinear if
Комментарии
 0:04:27
0:04:27
 0:02:34
0:02:34
 0:08:55
0:08:55
 0:03:14
0:03:14
 0:02:58
0:02:58
 0:06:13
0:06:13
 0:10:31
0:10:31
 0:04:01
0:04:01
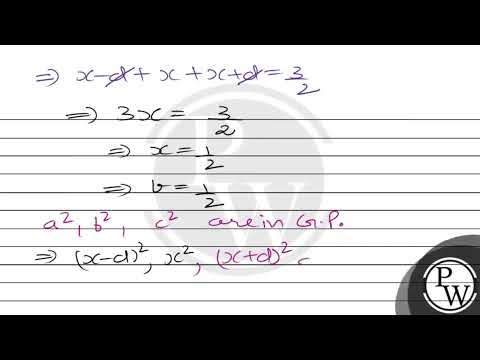 0:04:58
0:04:58
 0:06:55
0:06:55
 0:06:20
0:06:20
 0:04:01
0:04:01
 0:03:20
0:03:20
 0:03:30
0:03:30
 0:12:13
0:12:13
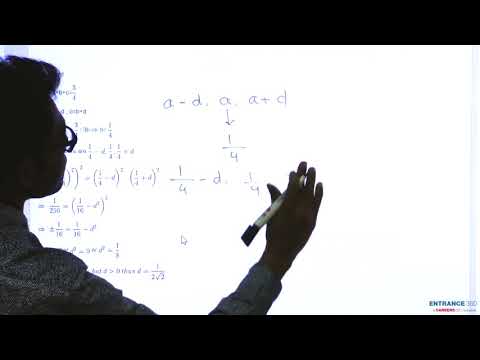 0:03:16
0:03:16
 0:03:38
0:03:38
 0:04:51
0:04:51
 0:07:18
0:07:18
 0:01:26
0:01:26
 0:01:09
0:01:09
 0:06:28
0:06:28
 0:05:00
0:05:00
 0:05:42
0:05:42