filmov
tv
Limit of an integral function

Показать описание
In this video, I showed how to find the limit of an integral function using FTC
Limit of an integral function
limit, derivative, integral all in one!,
Calculus - Definite Integrals
How to Find a Definite Integral using Riemann Sums and the Limit Definition: Quadratic Example
Finding The Area Using The Limit Definition & Sigma Notation
Limit problem with Fundamental Theorem of Calculus
Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
Limit as an integral (Riemann Sum)
How to find the Volume under the surface of a Cone using double integration
Calculus 1 - Introduction to Limits
Improper Integrals - Convergence and Divergence - Calculus 2
Converting a Riemann Sum to a Definite Integral
Definite integral as the limit of a Riemann sum | AP Calculus AB | Khan Academy
Worked example: Rewriting limit of Riemann sum as definite integral | AP Calculus AB | Khan Academy
IIT JEE Integral Limit
Region, Riemann sum, and integral!
Fundamental Theorem of Calculus Part 1
Definite Integral
Calculus - How to find the bounds of a triple integral
Integral of ln(x) fast!
Integral with a limit
The Leibniz rule for integrals: The Derivation
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus
Introduction to limits | Limits | Differential Calculus | Khan Academy
Комментарии
 0:07:27
0:07:27
 0:08:29
0:08:29
 0:07:15
0:07:15
 0:13:18
0:13:18
 0:13:18
0:13:18
 0:12:59
0:12:59
 0:20:46
0:20:46
 0:06:57
0:06:57
 0:08:42
0:08:42
 0:20:20
0:20:20
 0:13:56
0:13:56
 0:03:13
0:03:13
 0:04:26
0:04:26
 0:06:35
0:06:35
 0:07:05
0:07:05
 0:00:30
0:00:30
 0:11:30
0:11:30
 0:11:05
0:11:05
 0:04:56
0:04:56
 0:00:45
0:00:45
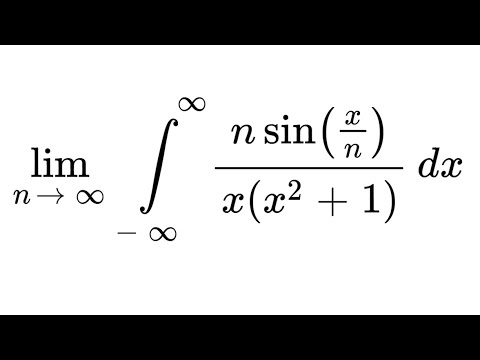 0:10:04
0:10:04
 0:17:40
0:17:40
 0:18:27
0:18:27
 0:11:32
0:11:32