filmov
tv
The Leibniz rule for integrals: The Derivation

Показать описание
Help me create more free content! =)
Today's video is going to be exciting! W are going to derive the Leibniz Rule for integrals in its whole form! It's one of the most powerful tools of integration, so be prepared! :)^
Quick note: The Integral I(x,t) is just in terms of t, so it's I(t) thanks for noticing! Even though, it doesn't quite matter, since we are just differentiating by t^^
Visit my website! =)
The Leibniz rule for integrals: The Derivation
Leibniz integral rule
Fundamental Theorem of Calculus Part 1
Integration: Leibniz Integral Rule
Leibniz Integral Rule - updated! 💪
The Leibniz Rule for Differentiation Under the Integral Sign
The leibniz integral rule (part-1)
Leibniz Integral Rule - Integral of (x^(e-1)-1)/ln(x)
'Mastering Leibniz Rule for JEE Advanced | Taught by an IITian 🚀'
Leibniz Integral Rule Quiz
Leibniz's Rule - 12 Integrals, Ep. 4
leibniz rule I for Integrals
Leibniz Integral Rule and FTC Part II, Calculus 1
Differentiation under the Integral Sign Tutorial
Feynman's integration trick: Differentiating under the Integral sign | Leibniz Rule
What is integration? This video explains the concept of integration #calculus #integration
How REAL Men Integrate Functions
Derivation of Leibniz Integral Rule
Leibniz's Integral Rule
Leibniz' rule: Integration via differentiation under integral sign
Integration Basic Formulas
MIT- integration bee challenge problem - Leibniz integration rule
Leibniz integral rule for differentiation under the integral sign iit jam 2008 integral calculus
Leibniz Integral Rule | Lecture 6 | Integrals as functions of parameters | #3 Solved examples
Комментарии
 0:17:40
0:17:40
 0:09:25
0:09:25
 0:11:30
0:11:30
 0:05:53
0:05:53
 0:11:18
0:11:18
 0:00:51
0:00:51
 0:08:56
0:08:56
 0:07:55
0:07:55
 0:20:47
0:20:47
 0:15:24
0:15:24
 0:05:56
0:05:56
 0:20:56
0:20:56
 0:04:18
0:04:18
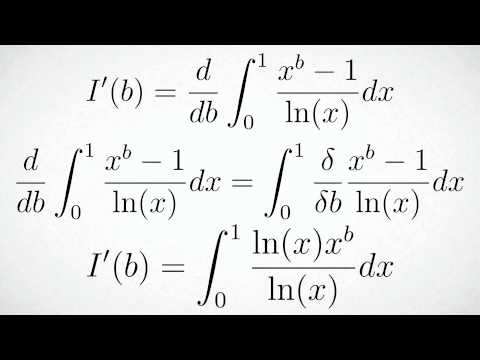 0:08:21
0:08:21
 0:21:56
0:21:56
 0:00:44
0:00:44
 0:00:35
0:00:35
 0:20:11
0:20:11
 0:04:43
0:04:43
 0:05:39
0:05:39
 0:00:05
0:00:05
 0:06:05
0:06:05
 0:01:34
0:01:34
 0:12:32
0:12:32