filmov
tv
International Mathematics Competition 2020 Day 2 Problem 1 | A Derivative Inequality
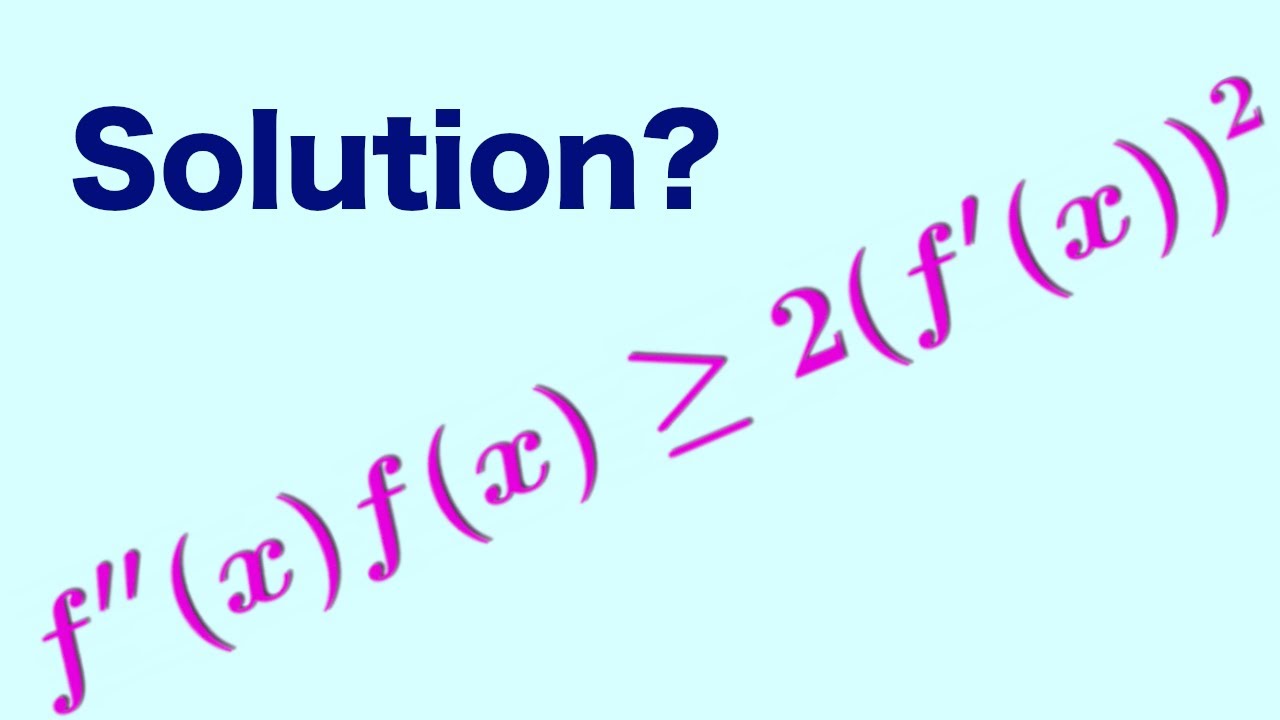
Показать описание
This video discusses an interesting differential inequality that appeared on the 2020 International Mathematics Competition. It showcases both how to develop intuition for inequalities involving derivatives, and how to interpret the results from these geometrically.
#Inequalities #MathematicsCompetitions #DifferentialCalculus
GET MY BOOK ON AMAZON!!
========================
"Number Theory Towards RSA Cryptography in 10 Undergraduate Lectures"
CHECK OUT OTHER TYPES OF VIDEOS:
================================
Improve Your Putnam Math Competition Performance:
------------------------------------------------------
Math Theorems:
------------------------------------------------------
GRE Math Subject Test:
------------------------------------------------------
Road to RSA Encryption:
-------------------------------------------------------
CHECK ME OUT ON THE INTERNET!!
==============================
Twitter: @mohamedomarphd
Instagram: profomarmath
And of course, subscribe to my channel!
#Inequalities #MathematicsCompetitions #DifferentialCalculus
GET MY BOOK ON AMAZON!!
========================
"Number Theory Towards RSA Cryptography in 10 Undergraduate Lectures"
CHECK OUT OTHER TYPES OF VIDEOS:
================================
Improve Your Putnam Math Competition Performance:
------------------------------------------------------
Math Theorems:
------------------------------------------------------
GRE Math Subject Test:
------------------------------------------------------
Road to RSA Encryption:
-------------------------------------------------------
CHECK ME OUT ON THE INTERNET!!
==============================
Twitter: @mohamedomarphd
Instagram: profomarmath
And of course, subscribe to my channel!
International Mathematics Competition 2020 Day 2 Problem 1 | A Derivative Inequality
Young lady absolutely kills it in Nigerian Maths Competition!
Chinese IMO team
Top 20 (1991-2020) Gold Medals in IMO : International Competition of Mathematics
Math Olympiad Awards 2020
International Mathematical Contest Questions | IMO | PMWC | IMC l Mathematics Olympiad
HOW CHINESE STUDENTS SO FAST IN SOLVING MATH OVER AMERICAN STUDENTS
MIT is first to solve problem C
NEP 2020- Project Based Learning -Mr Deepak Waikar,Singapore
Luxembourg - Math Olympiad Question | You should know this trick
How to solve math problems in IMC (International Mathematics Competition) Part 1 Episode 1
International Singapore Maths Competition 2020
IYMC | International Youth Math Challenge 2020 | Full Information
Differential Calculus Problem IMC
Look now, Student Abacus solves the biggest math calculations in just a few seconds #maths #shorts
26th International Mathematics Competition for University Students 2019 - MatIME
American mathletes come in 4th place in International Mathematical Olympiad
INTERNATIONAL OLYMPIAD IN INFORMATICS COMPETITION TOTAL MEDALS | LOOKER
Number theory questions in two different competitions (IMSO2020 vs SMO20201 Open)
JUARA INTERNATIONAL KANGAROO MATHEMATICS CONTEST 2020
Mathematics | Mathematics Competition | I-EMC 2020 Testimony
Harvard University is first to solve problem A
Harvard MIT Mathematical Tournament | HMMT-2020| School of Olympiad (L-13)
International Youth Math competition 2020 Solution Part 2
Комментарии
 0:10:24
0:10:24
 0:01:35
0:01:35
 0:00:34
0:00:34
 0:01:40
0:01:40
 0:05:35
0:05:35
 0:01:01
0:01:01
 0:00:23
0:00:23
 0:00:28
0:00:28
 0:46:23
0:46:23
 0:02:51
0:02:51
 0:09:42
0:09:42
 0:00:58
0:00:58
 0:04:27
0:04:27
 0:13:16
0:13:16
 0:00:31
0:00:31
 0:01:58
0:01:58
 0:02:11
0:02:11
 0:02:51
0:02:51
 0:06:10
0:06:10
 0:01:28
0:01:28
 0:01:33
0:01:33
 0:00:35
0:00:35
 0:06:42
0:06:42
 0:05:12
0:05:12