filmov
tv
Solving A Polynomial Equation with Radicals
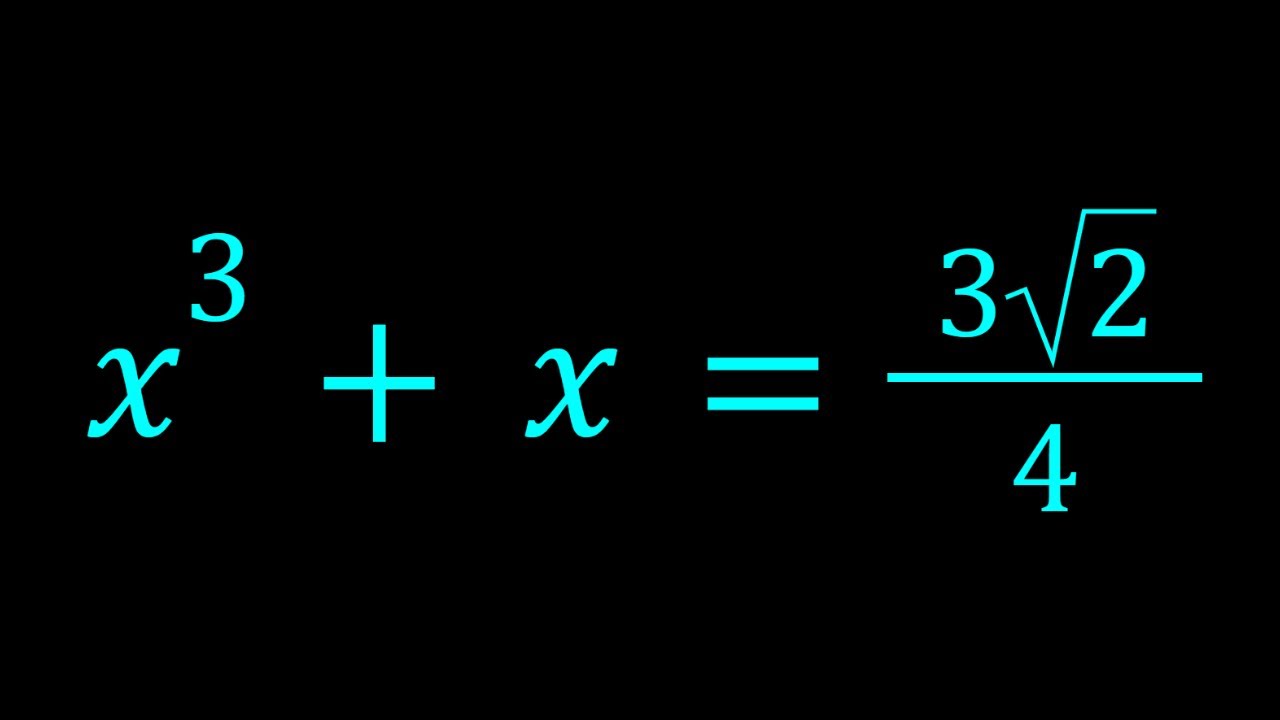
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #Polynomials #PolynomialEquations
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #Polynomials #PolynomialEquations
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving Polynomial Equations By Factoring and Using Synthetic Division
Solving Polynomial Equations - Grade 10 Math
Solving Polynomial Equations (1 of 2: Using the factor theorem)
How To Solve a Polynomial Equation Raised to the Fourth Power
Solving Polynomial Equations Algebraically
Finding All Zeros of a Polynomial Function Using The Rational Zero Theorem
How to factor a hard 4th degree polynomial (no rational zero, can't do it by grouping)
Polynomial Equations in Factored Form
solve quadratic equation #shortsfeed #shorts
Solving A Polynomial Equation with Radicals
How To Factor Polynomials The Easy Way!
Solving a Polynomial System of Equations
17 - Solve Polynomial Equations & Roots of a Polynomial, Part 1
Quadratic Equations | Solve by factoring | Free Math Videos
Algebra Basics: What Are Polynomials? - Math Antics
How to Solve a Polynomial Equation
Solving Higher-Degree Polynomials by Synthetic Division and the Rational Roots Test
Solving Polynomial Equations by Graphing | Polynomials Equations |
Learn How to Solve a Polynomial Equation to a Higher Degree by Factoring
Factoring & Solving Polynomial Equations (Learn Algebra 2)
How To Graph Polynomial Functions Using End Behavior, Multiplicity & Zeros
SHS 1 Elective Math - How To Solve Polynomial Functions
Casio fx-991MS - Solve a polynomial
How To Solve Quadratic Equations By Factoring - Quick & Simple! | Algebra Online Course
Комментарии
 0:14:19
0:14:19
 0:12:02
0:12:02
 0:09:20
0:09:20
 0:04:52
0:04:52
 0:30:31
0:30:31
 0:12:18
0:12:18
 0:04:55
0:04:55
 0:09:29
0:09:29
 0:01:01
0:01:01
 0:10:39
0:10:39
 0:11:54
0:11:54
 0:11:00
0:11:00
 0:37:37
0:37:37
 0:02:43
0:02:43
 0:11:09
0:11:09
 0:04:42
0:04:42
 0:09:22
0:09:22
 0:15:43
0:15:43
 0:06:25
0:06:25
 0:17:57
0:17:57
 0:20:28
0:20:28
 0:14:16
0:14:16
 0:00:27
0:00:27
 0:12:29
0:12:29