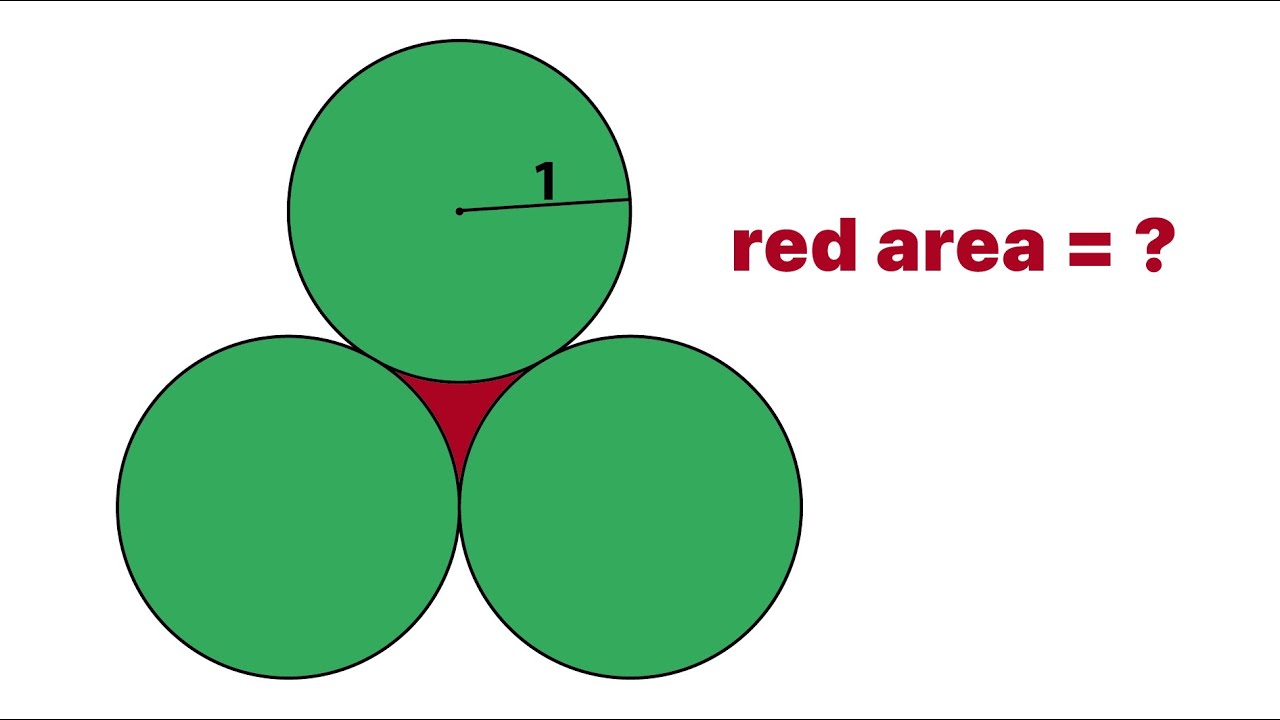
Find the area of the red region?

Three identical green circles with radius of 1, are placed tangent to each other, as shown in this diagram. Find the area of the red region.

[sans]

draw a triangle around the area consisting of the centerpoints of each circle. this triangle has all sides=2. it’s equilateral so each angle is 60°. red area = area of the equilateral triangle - 3*(area of a green circle segment)
each angle=60° and 60=(1/6)360
=> area of a segment=(1/6)(pi*r^2)=pi/6
=>3*(area of a green circle segment)=3pi/6=pi/2
==area of the triangle==
the area is bh/2, b=2,
=>area of the triangle=2(sqrt3)/2=sqrt3
=>area of red=sqrt3-pi/2≈0.1613

[devondevon]

0.161
Draw an equilateral triangle by connecting the three circles' centers. Its area is sqrt 3 or (1.73205)
Each circle area is pi or 3.1415. Since the equilateral triangle angles are 60 degrees, then
each circle contributed 1/6 of its area to the triangle, hence divide 3.1415 by 6 = 0.5236.
Since there are three, multiply 0.5236 by 3 =1.5708. This means that three total area
of the green inside the equilateral triangle is 1.5708 square units.
Since the area of the equilateral triangle is 1.73205, then the area of the red
is 1.73205 - 1.5708 = 0.161 Answer