filmov
tv
Extended Euclidean Algorithm in Cryptography and network security to Find GCD of 2 numbers examples

Показать описание
Extended euclidean algorithm is explained here with a detailed example of finding GCD of 2 numbers using extended euclidean theorem in cryptography. In this video of CSE concepts with Parinita Hajra, we will see about how to find out GCD of 2 numbers using Extended Euclidean Algorithm #gcd #greatestcommondivisor #extendedEuclidean #cseconceptwithparinita
For the people asking me for the equipments I use.... you can buy them from the below links:
If you like my video contents, please LIKE, COMMENT, SUBSCRIBE and SHARE with your friends.
You can always connect with me at:
Compiler design tutorials:
Theory of computation (TOC) tutorials:
Cryptography techniques tutorials:
Artificial Intelligence tutorials:
GATE previous year important questions:
Data Compression tutorials:
Computer networks tutorials:
Technical job updates:
Data structures and Algorithms tutorials:
Programming questions:
Digital image processing:
Digital electronics:
Motivational videos:
Keep learning, keep supporting 🤝✨💯
For the people asking me for the equipments I use.... you can buy them from the below links:
If you like my video contents, please LIKE, COMMENT, SUBSCRIBE and SHARE with your friends.
You can always connect with me at:
Compiler design tutorials:
Theory of computation (TOC) tutorials:
Cryptography techniques tutorials:
Artificial Intelligence tutorials:
GATE previous year important questions:
Data Compression tutorials:
Computer networks tutorials:
Technical job updates:
Data structures and Algorithms tutorials:
Programming questions:
Digital image processing:
Digital electronics:
Motivational videos:
Keep learning, keep supporting 🤝✨💯
Extended Euclidean Algorithm (Solved Example 1)
The Extended Euclidean algorithm
Extended Euclidean Algorithm Example
Extended Euclidean Algorithm - Example (Simplified)
Extended Euclidean Algorithm and Inverse Modulo Tutorial
Extended Euclidean Algorithm in Cryptography | Abhishek Sharma
The Extended GCD Algorithm
Extended Euclidean Algorithm using Example Multiplicative inverse of a number | Cryptography
Extended Euclidean Algorithm
Extended Euclidean Algorithm (Solved Example 3)
Extended Euclidean Algorithm - Cryptography - Cyber Security - CSE4003
2.2 Extended Euclidean Algorithm | CP Algorithm | Codenzyme
GCD, Bezout, and Modular Inverses | The Extended Euclidean Algorithm
Extended Euclidean Algorithm
Extended Euclidean Algorithm Explained
Number theory and Cryptography - Extended Euclidean Algorithm
The extended Euclidean algorithm | Math 361
Chapter 1 - Extended Euclid Algorithm example 2 : 85 and 37
extended euclidean algorithm ( in bangla )
How Does Euclid’s Algorithm Give HCF? | Euclid's Algorithm To Find HCF | BYJU'S Maths
Finding inverses by Extended Euclidean Algorithm .Cryptography . Easiest explanation ever
inverse modulo
Extended Euclidean Algorithm (in C++)
Extended Euclid Algorithm to solve 201x+81y=3
Комментарии
 0:10:16
0:10:16
 0:12:11
0:12:11
 0:14:50
0:14:50
 0:07:40
0:07:40
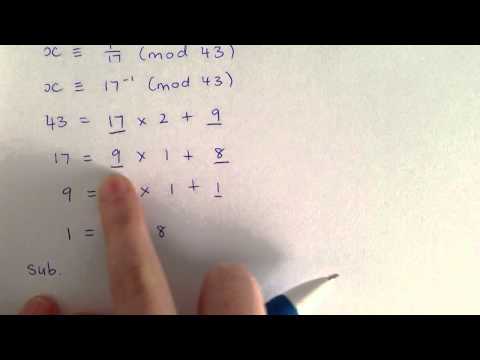 0:06:00
0:06:00
 0:11:19
0:11:19
 0:15:19
0:15:19
 0:04:24
0:04:24
 0:11:54
0:11:54
 0:06:54
0:06:54
 0:14:34
0:14:34
 0:11:31
0:11:31
 0:22:21
0:22:21
 0:02:42
0:02:42
 0:06:21
0:06:21
 0:09:01
0:09:01
 0:39:06
0:39:06
 0:07:32
0:07:32
 0:07:55
0:07:55
 0:00:20
0:00:20
 0:10:00
0:10:00
 0:00:15
0:00:15
 0:11:34
0:11:34
 0:05:46
0:05:46