filmov
tv
Improper Integrals: Example 3: 1/(1+x^2)

Показать описание
In this video I go over another example on improper integrals and this time solve the integral of the function 1/(1+x^2) from x approaches negative infinity to x approaches positive infinity. This integral can be simplified into two parts by integrating it from negative infinity until a number, chosen as zero in this example for convenience, and then from that number to positive infinity. This integral is very interesting as it converges at both positive and negative infinity resulting in the integral, and thus the area under the curve, to be equal to the number π.
Related Videos:
------------------------------------------------------
Related Videos:
------------------------------------------------------
Improper Integrals: Example 3: 1/(1+x^2)
Improper Integrals - Convergence and Divergence - Calculus 2
Testing Convergence of an Improper Integral: Example with 1/(x^3 + 1) from 1 to Infinity
The Improper Integral of 1/x^(2/3) from -1 to 1
Use comparison test to determine if improper integral dx/(x^3 +1) converges or diverges
Type 1 improper integrals! calculus 2
Evaluate Improper Integral 1/(x^2 + x) dx over [1, infinity). Infinite Integration Limits
Improper Integrals of Type II (Discontinuous Integrand) in 12 Minutes
Determine whether each integral is convergent or divergent. Integral of 3 to infinity(1/(x-2)^3/2)dx
Comparison Test for Improper Integrals
Improper Integrals Example 4: 1/x^p
Calculus 2 Lecture 7.6: Improper Integrals
i did another 100 integrals!
Evaluating Improper Integrals
The Comparison Theorem for Improper Integrals | Step by Step Explanation | Math with Professor V
Constant for Convergent Improper Integral
Improper Integrals Example 5: 1/sqrt(x-2)
Comparison test for improper integrals ex 3, integral of 1/ln(x) from e to inf, calculus 2 tutorial
Improper Integrals of Type I (Infinite Intervals) in 12 Minutes
Evaluate Improper Integral dx/(x-2)^3/2) over [3, infinity). Infinite Integration Limits
Determine whether integral is convergent or divergent. Integral from 1 to infinity of (1/(2x+1)^3)dx
How To Evaluate Special Improper Integrals - p-integrals
Calculus 2 - Improper Integrals - Practice Problem
Ex 1: Improper Integrals
Комментарии
 0:11:33
0:11:33
 0:13:56
0:13:56
 0:05:01
0:05:01
 0:04:34
0:04:34
 0:02:58
0:02:58
 0:27:48
0:27:48
 0:04:41
0:04:41
 0:11:23
0:11:23
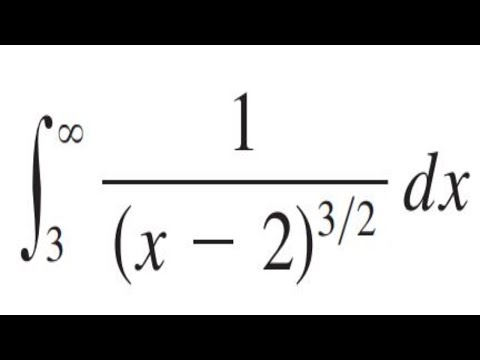 0:05:10
0:05:10
 0:12:53
0:12:53
 0:08:51
0:08:51
 2:48:31
2:48:31
 0:00:16
0:00:16
 0:12:24
0:12:24
 0:35:59
0:35:59
 0:14:10
0:14:10
 0:05:51
0:05:51
 0:11:07
0:11:07
 0:11:59
0:11:59
 0:03:06
0:03:06
 0:05:11
0:05:11
 0:14:55
0:14:55
 0:03:48
0:03:48
 0:04:21
0:04:21