filmov
tv
How to show vectors are orthogonal vectors using easy steps example (PART-4)

Показать описание
In this video explaining scalar product vector. In this example two vectors are given then prove vectors are orthogonal. This example is very simple using easy steps.
It's important to note that two non-zero vectors can be orthogonal only if they live in a space of at least two dimensions. In a one-dimensional space there is only one possible direction for a non-zero vector and it is not possible for two vectors to be orthogonal. In a two-dimensional space there are only two possible directions for non-zero vectors and they can be orthogonal if they are pointing in opposite directions. In higher-dimensional spaces there are more possible directions for non-zero vectors and the concept of orthogonality becomes more complex.
It's important to note that two non-zero vectors can be orthogonal only if they live in a space of at least two dimensions. In a one-dimensional space there is only one possible direction for a non-zero vector and it is not possible for two vectors to be orthogonal. In a two-dimensional space there are only two possible directions for non-zero vectors and they can be orthogonal if they are pointing in opposite directions. In higher-dimensional spaces there are more possible directions for non-zero vectors and the concept of orthogonality becomes more complex.
 0:04:41
0:04:41
 0:04:18
0:04:18
 0:17:42
0:17:42
 0:04:14
0:04:14
 0:04:29
0:04:29
 0:05:03
0:05:03
 0:09:03
0:09:03
 1:38:46
1:38:46
 0:09:17
0:09:17
 0:12:56
0:12:56
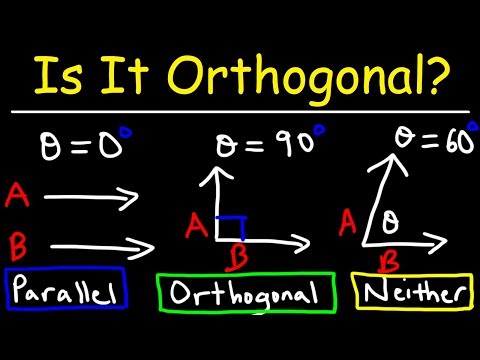 0:11:49
0:11:49
 0:10:06
0:10:06
 0:08:41
0:08:41
 0:09:59
0:09:59
 0:50:03
0:50:03
 0:04:41
0:04:41
 0:03:53
0:03:53
 0:01:08
0:01:08
 0:03:13
0:03:13
 0:04:31
0:04:31
 0:01:53
0:01:53
 0:13:46
0:13:46
 0:05:00
0:05:00