filmov
tv
Euclidean Division of Integers: Theorem and Proof
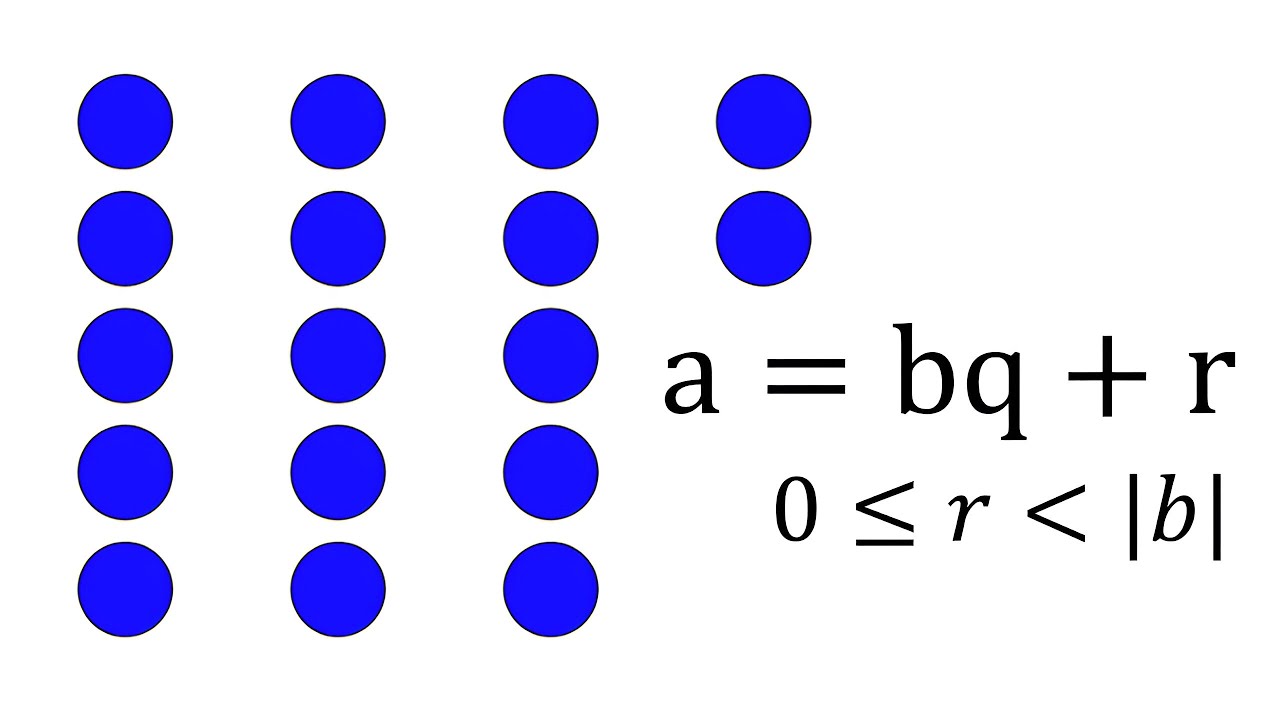
Показать описание
In this video I go over a pretty extensive “formal” proof of what otherwise seems to be a straight forward theorem known as the Euclidean Division. When an integer, known as the dividend, is divided by another integer, known as the divisor, we get an answer broken up into two parts. The first part is an integer known as the quotient that represents how many times the divisor can divide evenly into the dividend. The second part is the remaining fraction of the divisor that doesn’t divide cleanly, and in which the numerator is known as the Remainder. When working this out by hand such as the division 9/2 = 4+1/2 we can clearly see the breakdown of this division.
The formulization of this process is known as Euclidean Division of Integers, and the theorem is as follows: The division a/b of two integers, where b is not equal to zero, involves the existence and uniqueness of two integers q and r, such that a = bq + r for 0 ≤ r less than |b|. Now the proof of this theorem is also in the algorithm in obtaining these integers q and r. First I show that whether a or b are positive or negative, the theorem gets reduced to just the positive case. Working in an incremental step by step method, I show the Division Algorithm needed to obtain these numbers, thus proving their existence.
The uniqueness proof involves some out of the box thinking to first assume that there are other values that q and r can take to fit the theorem, but then showing that this is impossible. This is a very interesting part of the overall derivation so I highly recommend you watch and understand the very unique reasoning applied in it!
This is a very interesting and extensive proof video of a seemingly basic division procedure but its applications are far-reaching, so make sure to watch this video!
Video notes and playlist:
Related Videos:
------------------------------------------------------
The formulization of this process is known as Euclidean Division of Integers, and the theorem is as follows: The division a/b of two integers, where b is not equal to zero, involves the existence and uniqueness of two integers q and r, such that a = bq + r for 0 ≤ r less than |b|. Now the proof of this theorem is also in the algorithm in obtaining these integers q and r. First I show that whether a or b are positive or negative, the theorem gets reduced to just the positive case. Working in an incremental step by step method, I show the Division Algorithm needed to obtain these numbers, thus proving their existence.
The uniqueness proof involves some out of the box thinking to first assume that there are other values that q and r can take to fit the theorem, but then showing that this is impossible. This is a very interesting part of the overall derivation so I highly recommend you watch and understand the very unique reasoning applied in it!
This is a very interesting and extensive proof video of a seemingly basic division procedure but its applications are far-reaching, so make sure to watch this video!
Video notes and playlist:
Related Videos:
------------------------------------------------------
Комментарии
 0:45:20
0:45:20
 0:02:04
0:02:04
 0:05:50
0:05:50
 0:10:02
0:10:02
 0:14:38
0:14:38
 0:21:39
0:21:39
 0:02:23
0:02:23
 0:52:16
0:52:16
 1:14:15
1:14:15
 0:08:50
0:08:50
 0:12:12
0:12:12
 0:05:43
0:05:43
 0:10:00
0:10:00
 0:09:34
0:09:34
 0:12:11
0:12:11
 0:08:31
0:08:31
 0:05:15
0:05:15
 0:09:49
0:09:49
 0:02:42
0:02:42
 0:09:51
0:09:51
 0:06:58
0:06:58
 0:00:55
0:00:55
 0:01:53
0:01:53
 0:00:32
0:00:32