filmov
tv
The Chen Lu Equation

Показать описание
Here I solve an interesting question: For which f does the fake chen lu hold? In other words, for which f do we have (fog)'(x) = f'(x)g'(x) for all x. Watch this video to find out!
The Chen Lu Equation
When Dr. P discovered the “Chen Lu”
Use the Chen Lu
MOST REQUESTED CHEN LU PROBLEM!!!
Proof of the Chain Rule
Derivative of ln(ln(ln(x))) (feat. the Chen Lu)
Chain Rule Explained (with a box)
Lesson 31: Ex 1-3 Chen Lu Rule (Chain Rule). Methods of Differentiation
Chain Rule Challenge
Chen Lu is continuous
I can’t believe I made this mistake 😂
Putin flirts, Putin sigma rule, Putin body language #sigma #confidence #bodylanguage #putin #shorts
Lesson 22: Proof of the Quo Chen Lu Rule (Quotient Rule). Methods of Differentiation.
Lesson 32: Ex 4-7 Chen Lu Rule (Chain Rule) Methods of Differentiation
how not to solve a differential equation 😅
The Chain Rule
Lesson 30: Ex 1-5 of Quo Chen Lu Rule (Quotient Rule) Methods of Differentiation
Can you do these? Chain rule challenge with trig functions! Calculus 1
The worst book I bought because of BookTok
Cool Quotient Rule Proof
My pens vs the quadratic formula
Binomial Derivative
Alternatives to Chen Lu (Chain Rule), involving integration, FORM 5 SPM
Cool product rule proof
Комментарии
 0:03:01
0:03:01
 0:00:30
0:00:30
 0:00:51
0:00:51
 0:12:06
0:12:06
 0:16:05
0:16:05
 0:02:42
0:02:42
 0:06:54
0:06:54
 0:17:12
0:17:12
 0:21:03
0:21:03
 0:12:46
0:12:46
 0:00:26
0:00:26
 0:00:20
0:00:20
 0:25:00
0:25:00
 0:25:47
0:25:47
 0:03:56
0:03:56
 0:21:30
0:21:30
 0:22:35
0:22:35
 0:04:22
0:04:22
 0:00:15
0:00:15
 0:03:26
0:03:26
 0:00:24
0:00:24
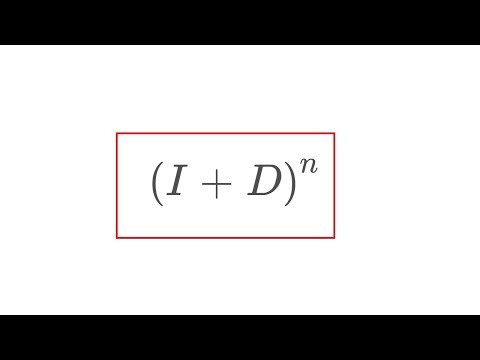 0:14:08
0:14:08
 0:16:54
0:16:54
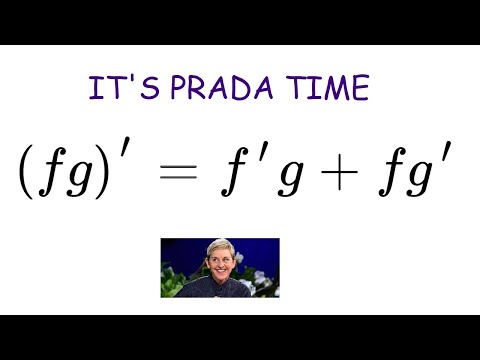 0:05:16
0:05:16