Complex Analysis 8 | Wirtinger Derivatives

Please consider to support me if this video was helpful such that I can continue to produce them :)

🙏 Thanks to all supporters! They are mentioned in the credits of the video :)

Thanks to all supporters who made this video possible! They are mentioned in the credits of the video :)

This is my video series about Complex Analysis. I hope that it will help everyone who wants to learn about complex derivatives, curve integrals, and the residue theorem. Complex Analysis has a lof applications in other parts of mathematics and in physics.

x

00:00 Intro
00:19 Wirtinger derivatives — basic definition
01:35 Complex derivative through Cauchy-Riemann equations
05:12 Wirtinger derivatives — detailed definition
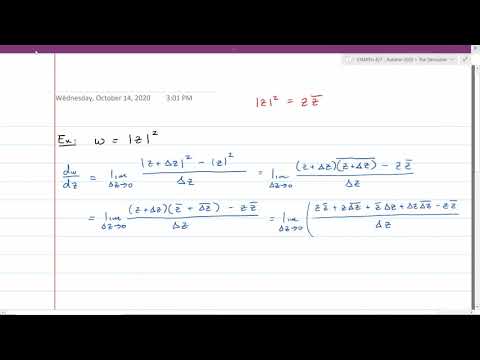
06:17 Example for z²
08:39 Summary: a criteria for holomorphic functions

#ComplexAnalysis
#Analysis
#Calculus
#Mathematics
#curveintegral
#integration

(This explanation fits to lectures for students in their first or second year of study: Mathematics, Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)

[niklasfi]

"We have learned in the last video that" f'(x+iy) = du/dx + i dv/dx. Where in the previous videos was this demonstrated? I can not see the connection. How does this follow from the Jacobian? Or is this a consequence of the function being analytic? If yes, how?

[qingninghuo]

There are quite a few comments regarding 02:19, f'(x+iy) = a+ib, where a=du/dx, b = dv/dx. Let's look at it this way.

Consider f(x+iy) = u(x, y)+iv(x, y), where u(x, y) and v(x, y) are the real and imaginary part of f, both of which are real valued functions. If f is complex differentiable, then the limit of (f(z+h)-f(z))/h should converge to a fixed value no matter which path h takes to converge to zero. So we could let h take the path along the real axis, in which case y could be considered as constant. We also have h=x and so dh=dx. Therefore we obtained f'(x+iy) = du/dx (x, y) + i dv/dx (x, y).

On the other hand, we could let h take the path along the y axis. Say h = yi, and so dh = dyi = idy. This would give us f'(x+iy) = -i du/dy (x, y) + dv/dy (x, y). Obviously this agrees with the above result due to the Cauchy Riemann equations.

[PunmasterSTP]

Wirtinger? More like "What a zinger!" These videos are all awesome; thanks for making and uploading them.

[NewDeal]

00:00 Intro
00:19 Wirtinger derivatives — basic definition
1:35 Complex derivative through CR equations
5:12 Wirtinger dericatives — detailed definition
6:17 Example for z^2
8:39 Summary: a criteria for holomorphic function

[alejrandom]

thank you so much for being on youtube

[satchelsieniewicz]

i think i understand because we can approach along any path choosing the partials with respect to x is just as valid as approaching with respect to y. for someone new to this it feels like you are omitting something when you just write it in terms of the x partials.

[individuoenigmatico]

I think the necessary and sufficient condition for holomorfic functions at the end should be that f is a totally differentiable function AND that ∂f/∂z̄=0. That is to say: f:U→ℂ is holomorfic in U iff f is totally differentiable in U AND [∂f/∂z̄](z)=0 for all z∈U.

Then to check for the total differentiability of f(x, y)=u(x, y)+i•v(x, y) we can use, as a sufficient condition, that all its partial derivatives (∂u/∂x, ∂v/∂x, ∂u/∂y and ∂v/∂y) are continuous in U.

[jfg]

I love the series! Super useful and super clear, thanks!

My question about this video: is it always possible to combine the d/dx and the d/dy and express the derivative in terms of just z?

[metuphys]

can you explain why is a=du/dx and b=dv/dx why not a=du/dy and b=dv/dy since the derivative is independent of the path taken

[jonasw]

I have been trying for a couple of hours to figure out why a=du/dx and b=dv/dx and read the comments that its just the jacobian, but I dont understand the relation how we conclude that? Can you please explain a little further or give me some text where its explained a little longer? Thanks a lot!

[gabrieletrovato]

2:17 Why d/dx and not for example d/dy? Are they the same? Perhaps d/dx = d/d(iy) ?

[diracbach]

i have a very similar question, to the one people has already made. I understand that in the Jacobi matrix a = du/dx and b is dv/dx but I don't see the connection between the Jacobian and this new notation. In other words why is the a and b of the Jacobian the same variables that we get here. how are they related?

[stearin]

Are z and z* independent variables? Can I prove diff-ity of z^2 just by saying that dz/dz*=0?

[froggieperi]

Hi, how do we watch the unavailable/hidden videos?

[zlatanbrekke]

I dont think I understand why f'(z_0) = a + ib