filmov
tv
Limit of (x^3 + 5x)/(2x^3 - x^2 + 4) as x approches infinity
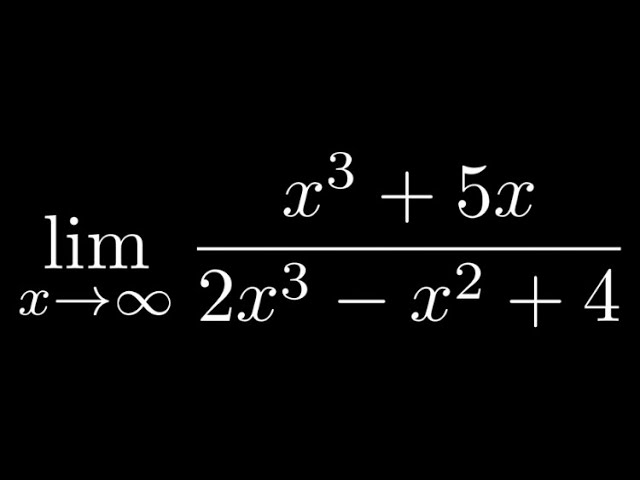
Показать описание
Limit of (x^3 + 5x)/(2x^3 - x^2 + 4) as x approches infinity. This is a calculus problem where we find the limit of a rational function.
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
Limit of (x^3 + 5x)/(2x^3 - x^2 + 4) as x approches infinity
Find the limit as x approaches infinity for (5x^3+2x)/(2x^3-4x^2+ 5x)
Learn how to evaluate a limit at infinity
Limit of (2x+5)/(3x+2) as x approaches positive infinity, done at three levels of understanding
Lím (x^3+5x)/(2x^3-x^2+4) cuando x tiende a infinito LÍMITE de una función EJERCICIOS RESUELTOS
lim┬(x→3)〖(2x^3-5x^2-2x-3)/(4x^3-13x^2+4x-3)〗- calculo 1
Evaluating Limits By Factoring
How To Find The Limit At Infinity
Turunan Pertama Fungsi Aljabar MATEMATIKA TINGKAT LANJUT KELAS 12 Soal Bagian A Halaman 175
Find the Limit of (x + x^3 + x^5)/(1 - x^2 + x^4) as x approaches Infinity
Find the limit as x approaches infinity of (3x^3 -2x+4)/(x^2 +1).
Limits Calculator Technique
Evaluate : lim (x→1) (x⁴ - 3x² + 2) / (x³ - 5x² + 3x + 1)
Finding a Limit by Factoring a Rational Function: (x^2 -2x - 3)/(x - 3) as x approaches 3
How to Write epsilon, delta-Proof for Limit of x^3 as x approaches -2
limit x mendekati 3 (5x-3)/√(x²+2x-6) | Kelas 11 #limit#shorts#kelas11
Find the limit as x approaches infinity of (2x -3)/(3x^2 -2x -2x +1)
Limites Cálculo 1 - Exercícios Resolvidos f(x)=(x^3 - 4x + 3)/(x^5 - 2x + 1)
limit (3x+5)/(2x-7) as x goes to infinity
Límites algebraicos - Ejercicio 6
Evaluating Limits - Basic Calculus
Piecewise Functions - Limits and Continuity | Calculus
5 simple unsolvable equations
Find the limit as x approaches infinity of (sqrt(x^2 + 2x +3) -x).
Комментарии
 0:02:36
0:02:36
 0:02:13
0:02:13
 0:01:40
0:01:40
 0:05:13
0:05:13
 0:09:29
0:09:29
 0:06:48
0:06:48
 0:11:35
0:11:35
 0:13:14
0:13:14
 0:11:07
0:11:07
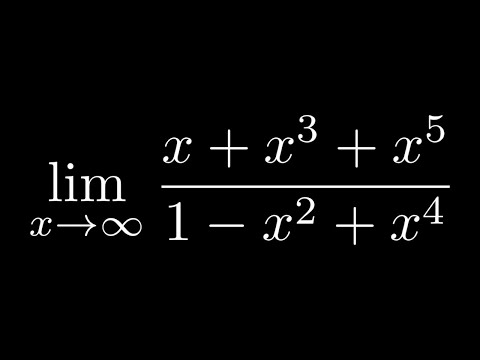 0:01:21
0:01:21
 0:02:31
0:02:31
 0:01:49
0:01:49
 0:07:12
0:07:12
 0:02:13
0:02:13
 0:02:45
0:02:45
 0:00:32
0:00:32
 0:02:02
0:02:02
 0:11:11
0:11:11
 0:01:50
0:01:50
 0:08:44
0:08:44
 0:06:25
0:06:25
 0:10:06
0:10:06
 0:00:50
0:00:50
 0:04:46
0:04:46