filmov
tv
This Sum Amazes Me Every Time
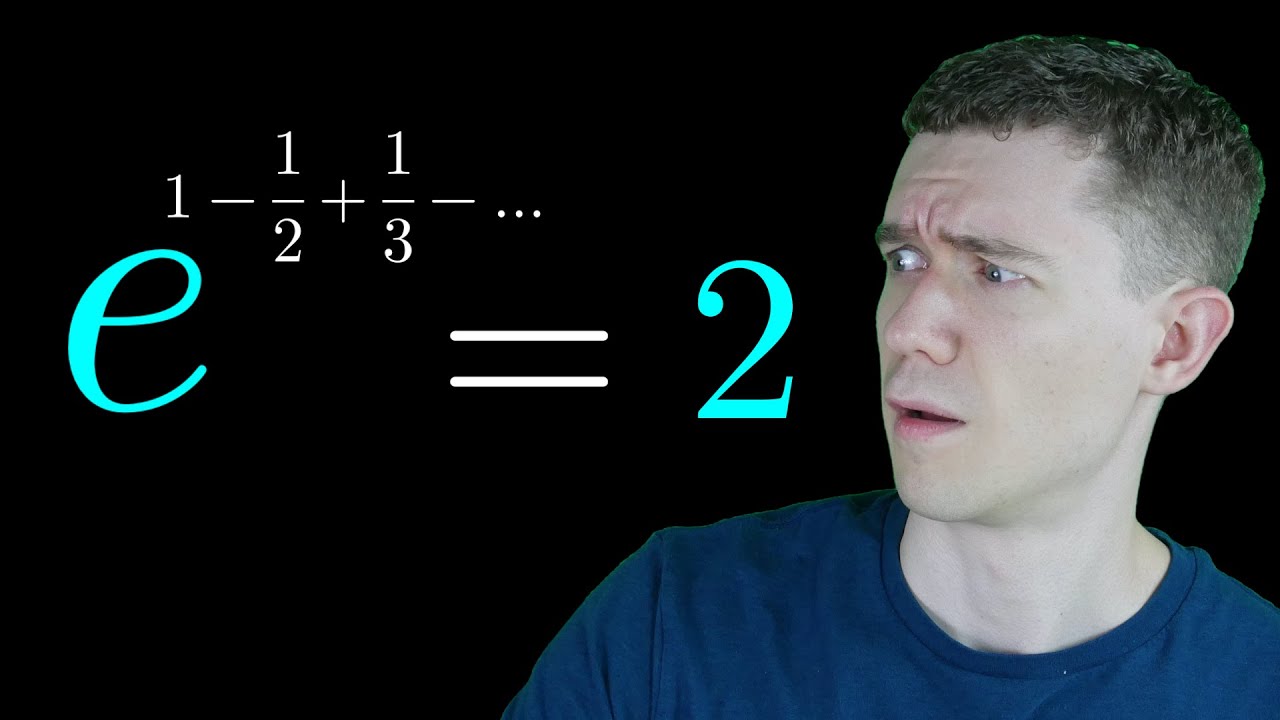
Показать описание
The Alternating Harmonic Series convergence is something you could show in a calc 2 class. Although the alternating harmonic series is conditionally convergent, you may not have known why the sum of alternating harmonic series equals ln2.
Time to look at an amazing alternating harmonic series proof!
🙏Support me by becoming a channel member!
#math #brithemathguy #alternatingharmonicseries
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information.
Time to look at an amazing alternating harmonic series proof!
🙏Support me by becoming a channel member!
#math #brithemathguy #alternatingharmonicseries
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information.
This Sum Amazes Me Every Time
Fan surprises Drake with this 😱
When Your Phone is at 1%...
Revolutionary Everyday Products You'll Be Amazed By
You Might Be Making This Mistake
The amount of y’all running there with me always amazes me 😭♥️
Easy Math trick to amaze your friends | Fun Trick | Limited to only some specific numbers!
EVERYONE is talking about THIS trick💥(EVERYONE is AMAZED)🤯
Why is dry ice so dangerous? | #aumsum #kids #science #education #children
This Still Surprises me Every Year in Germany!
Daughter Surprises Dad with His Own Movie! *emotional*
#essencepartner cosmetics , you NEVER fail to amaze me 😭❤️ #fyp #mascara #lashes
Daughter Surprises Mom with Her Own Movie! *emotional*
YOU will be AMAZED🤩
This Short May Amaze You - Wow! #wow
Andrea Ghez: 'It amazes me every time I go to the telescope'
Things You Do Wrong Every Day
Sometimes, the amount of impact my content can have amazes me.
The Best Volleyball Block Ever: Get Ready to Be Amazed
super natural jensen amazed by the amount of covid babies there are lmao #jensenackles #spnfamily
15 Easy Magic Tricks to Amaze Your Friends
I Tried EVERY VIRAL RECIPE off TIKTOK / INSTAGRAM (so you don't have to)
Summing The Alternating Harmonic Series
👀🤯AMAZED AT UR WISDOM FROM GOD|THEY MUST LET U GO IN PEACE|UR SUFFERING HAS THEM DO/GIVEU 2X AS MUCH...
Комментарии
 0:04:21
0:04:21
 0:00:30
0:00:30
 0:01:35
0:01:35
 0:22:28
0:22:28
 0:08:01
0:08:01
 0:00:11
0:00:11
 0:00:22
0:00:22
 0:01:28
0:01:28
 0:00:56
0:00:56
 0:07:16
0:07:16
 0:11:23
0:11:23
 0:00:25
0:00:25
 0:08:22
0:08:22
 0:00:48
0:00:48
 0:00:05
0:00:05
 0:06:21
0:06:21
 0:21:33
0:21:33
 0:00:57
0:00:57
 0:00:13
0:00:13
 0:00:57
0:00:57
 0:14:30
0:14:30
 0:25:32
0:25:32
 0:09:32
0:09:32
 1:04:33
1:04:33