Alternating Series Test (AST) - Alternating Harmonic Series | Series | Calculus | Glass of Numbers

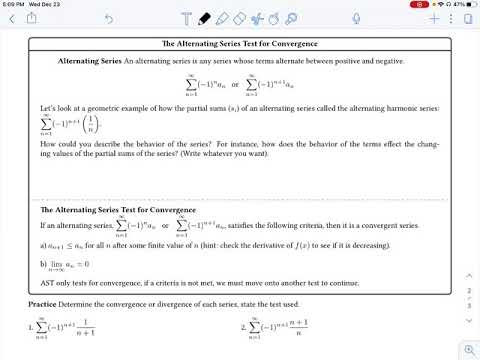
For alternating series, we can use the Alternating Series Test (AST) to show that it converges by checking the two conditions of AST:

1) The portion b_n of the terms (without the alternating factor) must be decreasing.
2) The limit of b_n is 0 as n approaches infinity.

Even though the harmonic series is divergent, this alternating harmonic series converges.

Please subscribe to my channel! Thank you!

Follow me: