filmov
tv
Magnitude, Ratio, and Proportion

Показать описание
In today's video, I discussed Magnitude, Ratio, and Proportion. A magnitude is the idea of size, dimension, or extent. We ask questions such as "How far?", "How heavy?", etc. A ratio is literally a comparison of magnitudes. This is required in order to distinguish the antecedent magnitude from other magnitudes. By convention, the antecedent magnitude is the primary magnitude of concern in any ratio, whereas the consequent magnitude is auxiliary. This kind of comparison is purely qualitative in terms of measure and is not necessarily accurate or sufficient. The Ancient Greeks could have chosen the other way round and it wouldn't have made any difference, that is, ratio = consequent : antecedent. But, remember that the accepted way is: ratio = antecedent : consequent. The Greeks chose line segments because these were the easiest to compare! A proportion is best described by a comparison of two ratios of magnitudes. Whilst a proportion exists between the aliquot parts of each ratio, one cannot tell much about the proportion until it is compared to a third ratio. The third ratio might consist of the aliquot parts' sum or difference. If not, then at the very minimum three magnitudes are required to gain an understanding of the proportion. This principle precedes the realisation of the abstract unit in algebra and the establishment of the well-defined number concept. Please leave any questions or comments for this video. Thank you for watching.
 0:17:52
0:17:52
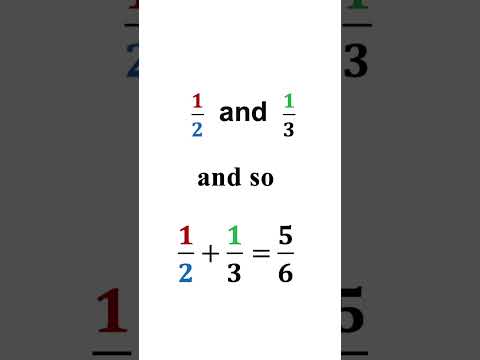 0:00:46
0:00:46
 0:07:02
0:07:02
 0:13:53
0:13:53
 0:02:41
0:02:41
 0:00:34
0:00:34
 0:04:09
0:04:09
 0:12:08
0:12:08
 1:19:40
1:19:40
 0:03:27
0:03:27
 0:02:54
0:02:54
 0:37:56
0:37:56
 0:10:25
0:10:25
 1:52:50
1:52:50
 0:04:51
0:04:51
 1:09:27
1:09:27
 0:53:59
0:53:59
 0:13:17
0:13:17
 0:00:46
0:00:46
 0:11:07
0:11:07
 0:24:20
0:24:20
 0:00:20
0:00:20
 0:03:59
0:03:59